早教吧作业答案频道 -->数学-->
在平面直角坐标系xOy中,抛物线y=12x2-x+2与y轴交于点A,顶点为点B,点C与点A关于抛物线的对称轴对称.(1)求直线BC的解析式;(2)点D在抛物线上,且点D的横坐标为4.将抛物线在点A,D之
题目详情
在平面直角坐标系xOy中,抛物线y=
x2-x+2与y轴交于点A,顶点为点B,点C与点A关于抛物线的对称轴对称.
(1)求直线BC的解析式;
(2)点D在抛物线上,且点D的横坐标为4.将抛物线在点A,D之间的部分(包含点A,D)记为图象G,若图象G向下平移t(t>0)个单位后与直线BC只有一个公共点,求t的取值范围.
| 1 |
| 2 |
(1)求直线BC的解析式;
(2)点D在抛物线上,且点D的横坐标为4.将抛物线在点A,D之间的部分(包含点A,D)记为图象G,若图象G向下平移t(t>0)个单位后与直线BC只有一个公共点,求t的取值范围.
▼优质解答
答案和解析
(1)∵抛物线y=
x2-x+2与y轴交于点A,
∴点A的坐标为(0,2).
∵y=
x2-x+2=
(x-1)2+
,
∴抛物线的对称轴为直线x=1,顶点B的坐标为(1,
).
又∵点C与点A关于抛物线的对称轴对称,
∴点C的坐标为(2,2),且点C在抛物线上.
设直线BC的解析式为y=kx+b.
∵直线BC经过点B(1,
)和点C(2,2),
∴
解得
∴直线BC的解析式为:y=
x+1;
(2)∵抛物线y=
x2-x+2中,当x=4时,y=6,
∴点D的坐标为(4,6).
∵直线y=
x+1中,当x=0时,y=1.当x=4时,y=3,
∴如图,点E的坐标为(0,1),点F的坐标为(4,3).
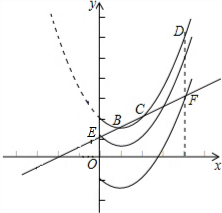
设点A平移后的对应点为点A′,点D平移后的对应点为点D′.当图象G向下平移至点A′与点E重合时,点D'在直线BC上方,
此时t=1.
当图象G向下平移至点D′与点F重合时,点A′在直线BC下方,此时t=3.
结合图象可知,符合题意的t的取值范围是1<t≤3.
| 1 |
| 2 |
∴点A的坐标为(0,2).
∵y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴抛物线的对称轴为直线x=1,顶点B的坐标为(1,
| 3 |
| 2 |
又∵点C与点A关于抛物线的对称轴对称,
∴点C的坐标为(2,2),且点C在抛物线上.
设直线BC的解析式为y=kx+b.
∵直线BC经过点B(1,
| 3 |
| 2 |
∴
|
解得
|
∴直线BC的解析式为:y=
| 1 |
| 2 |
(2)∵抛物线y=
| 1 |
| 2 |
∴点D的坐标为(4,6).
∵直线y=
| 1 |
| 2 |
∴如图,点E的坐标为(0,1),点F的坐标为(4,3).

设点A平移后的对应点为点A′,点D平移后的对应点为点D′.当图象G向下平移至点A′与点E重合时,点D'在直线BC上方,
此时t=1.
当图象G向下平移至点D′与点F重合时,点A′在直线BC下方,此时t=3.
结合图象可知,符合题意的t的取值范围是1<t≤3.
看了 在平面直角坐标系xOy中,抛...的网友还看了以下:
我急!二次函数的题,抛物y=ax方+bx+c与x轴交与点B(1,0),C(-3,0),且过点A(3 2020-05-13 …
用配方法把下列函数化成y=a(x+h)的平方+k的形式,并指出抛物线的开口方向,顶点坐标和对称轴 2020-05-16 …
已知抛物线y=ax^2+bx+c(a≠0)顶点(1,1)且过原点O.过抛物线上一点P(x,y)向知 2020-05-16 …
y=-1/2x2-x+2用配方法求出它的抛物线的顶点坐标和对称轴y=-1/2x2-x+2(y等于负 2020-05-24 …
用配方法求下列抛物线的顶点坐标和对称轴y=-3x²-2x+1,y=2x²+3x-1,y=-3x²+ 2020-05-24 …
已知抛物线与x轴只有一个交点(-2,0),且过点(0,1)求解析式已知抛物线的最低点坐标是(-1, 2020-06-18 …
将抛物线y等于2括号x减一括号的平方加三做下列移动,求得到的抛物线的解析式.以x轴为对称轴,将原抛 2020-07-10 …
抛物线关于直线对称求y^2=4x关于y=x+1的抛物线方程! 2020-07-20 …
平面直角坐标系的疑问..1.什么是横轴上的点,纵坐标为0.纵轴上的点,横坐标为0.2.什么是关于X 2020-07-30 …
(2012•江西模拟)甲、乙两同学对关于y、x的抛物线f:y=x2-2mx+2m2+2m进行探讨交流 2020-12-23 …