早教吧作业答案频道 -->数学-->
(本题满分12分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.求证:(1)、D是BC的中点;(2)、△BEC∽△ADC;(3)、若,求⊙O的半径。
题目详情
(本题满分12分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.

求证:(1)、D是BC的中点;(2)、△BEC∽△ADC;(3)、若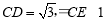 ,求⊙O的半径。
,求⊙O的半径。
▼优质解答
答案和解析
(1)、(2)略;(3)、3.
分 析:
(1)、根据直径所对的圆周角为直角得出AD为高线,然后根据等腰三角形的三线合一定理进行说明;(2)、根据同弧所对的圆周角相等得出∠CBE=∠CAD,然后根据∠BCE=∠ACD说明三角形相似;(3)、根据三角形相似进行求解.试题
解析:
(1)、证明:∵AB是⊙O的直径, ∴∠ADB=90° 即AD是底边BC上的高. 又∵AB=AC,∴△ABC是等腰三角形, ∴D是BC的中点(2)、证明:∵∠CBE与∠CAD是同弧所对的圆周角,∴ ∠CBE=∠CAD.又∵ ∠BCE=∠ACD, ∴△BEC∽△ADC;(3)、
由△BEC∽△ADC得:, 即CD·BC=AC·CE. ∵D是BC的中点,∴CD=BC.又 ∵AB=AC,∴CD·BC=AC·CE=BC ·BC=AB·CE 即BC=2AB·CE=12∴AB=6 ∴⊙O的半径为3……12分
考点:
圆的基本性质、三角形相似的判定与应用.
分 析:
(1)、根据直径所对的圆周角为直角得出AD为高线,然后根据等腰三角形的三线合一定理进行说明;(2)、根据同弧所对的圆周角相等得出∠CBE=∠CAD,然后根据∠BCE=∠ACD说明三角形相似;(3)、根据三角形相似进行求解.试题
解析:
(1)、证明:∵AB是⊙O的直径, ∴∠ADB=90° 即AD是底边BC上的高. 又∵AB=AC,∴△ABC是等腰三角形, ∴D是BC的中点(2)、证明:∵∠CBE与∠CAD是同弧所对的圆周角,∴ ∠CBE=∠CAD.又∵ ∠BCE=∠ACD, ∴△BEC∽△ADC;(3)、
由△BEC∽△ADC得:, 即CD·BC=AC·CE. ∵D是BC的中点,∴CD=BC.又 ∵AB=AC,∴CD·BC=AC·CE=BC ·BC=AB·CE 即BC=2AB·CE=12∴AB=6 ∴⊙O的半径为3……12分
考点:
圆的基本性质、三角形相似的判定与应用.
看了 (本题满分12分)如图,在△...的网友还看了以下:
线代,A为n阶方阵A^2-2A-3E=0求(A^2+A+E)^-12.设AB均为正交矩阵|A|=- 2020-04-12 …
已知P为圆外一点,PA,PB切⊙O于点A、B,OP与AB相交于点M,过点M作弦CD.求证:∠CPO 2020-04-27 …
命题:“若空间两条直线a,b分别垂直平面α,则a∥b”学生小夏这样证明:设a,b与面α分别相交于A 2020-05-13 …
向量证明三角形三条中线交于一点,1.证明三角形三条中线交于一点(以下字母全都表示向量)令AC=a, 2020-05-16 …
设A,B为n阶方阵,若AB=A+B,证明:A-E可逆,且AB=BA.这题怎样做啊? 2020-06-12 …
关于集合AB,A交B等于B并A是A等于B的什么条件 2020-06-23 …
1.如图,△ABC在平面a外,AB∩a=P,BC∩a=Q,AC∩a=R,求证:P,Q,R三点共线. 2020-07-31 …
一道有关集合的数学题设集合A的元素都是正整数,满足如下条件:(1)A的元素个数不小于3;(2)若a 2020-07-31 …
如图1,BC是O的直径,点A在O上,点D在CA的延长线上,DE⊥BC,垂足为点E,DE与O相交于点H 2020-11-03 …
已知abc两两相互独立,求证P(a交b交c)=p(a)p(b)p(c)已知ab相互独立,求证a已知a 2020-12-01 …