早教吧作业答案频道 -->数学-->
已知圆C:(x-1)2+y2=16,F(-1,0),M是圆C上的一个动点,线段MF的垂直平分线与线段MC相交于点P.(Ⅰ)求点P的轨迹方程;(Ⅱ)记点P的轨迹为C1,A、B是直线x=-2上的两点,满足AF⊥BF,曲
题目详情
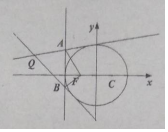
已知圆C:(x-1)2+y2=16,F(-1,0),M是圆C上的一个动点,线段MF的垂直平分线与线段MC相交于点P.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)记点P的轨迹为C1,A、B是直线x=-2上的两点,满足AF⊥BF,曲线C1与过A,B的两条切线(异于x=-2)交于点Q,求四边形AQBF面积的取值范围.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)记点P的轨迹为C1,A、B是直线x=-2上的两点,满足AF⊥BF,曲线C1与过A,B的两条切线(异于x=-2)交于点Q,求四边形AQBF面积的取值范围.
▼优质解答
答案和解析
 (Ⅰ)依题意得圆心C(0,1),半径r=4,
(Ⅰ)依题意得圆心C(0,1),半径r=4,
∵线段MF的垂直平分线与线段MC相交于点P,
∴|PF|+|PC|=|PM|+|PC|=CM=4>|CF|=2.
∴点P的轨迹方程是以C,F为焦点,长轴长为4的椭圆,
即a=2,c=1,则b=22-1=3,
∴P的轨迹方程是
+
=1.
(Ⅱ)依题意,直线AF斜率存在且不为零,设为y=k(x+1),
令x=-2得A(-2,-k),同理B(-2,
).
设过点A的切线为y=k1(x+2)-k,代入
+
=1
得(3+4k12)x2+8k1(2k1-k)x+4(2k1-k)2-12=0x+4[(2k1-k)2-3]=0.
由△=64k12(2k1-k)2-16(3+4k12)[(2k1-k)2-3]=0,解得k1=
,
同理k2=
=
.
联立方程组:
,解得x=-4.
∴SAQBF=
|AB||xF-xQ|=
|k+
|≥3,当且仅当k=±1时等号成立,
∴四边形AQB
 (Ⅰ)依题意得圆心C(0,1),半径r=4,
(Ⅰ)依题意得圆心C(0,1),半径r=4,∵线段MF的垂直平分线与线段MC相交于点P,
∴|PF|+|PC|=|PM|+|PC|=CM=4>|CF|=2.
∴点P的轨迹方程是以C,F为焦点,长轴长为4的椭圆,
即a=2,c=1,则b=22-1=3,
∴P的轨迹方程是
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)依题意,直线AF斜率存在且不为零,设为y=k(x+1),
令x=-2得A(-2,-k),同理B(-2,
| 1 |
| k |
设过点A的切线为y=k1(x+2)-k,代入
| x2 |
| 4 |
| y2 |
| 3 |
得(3+4k12)x2+8k1(2k1-k)x+4(2k1-k)2-12=0x+4[(2k1-k)2-3]=0.
由△=64k12(2k1-k)2-16(3+4k12)[(2k1-k)2-3]=0,解得k1=
| k2-3 |
| 4k |
同理k2=
(-
| ||
4•(-
|
| 3k2-1 |
| 4k |
联立方程组:
|
∴SAQBF=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| k |
∴四边形AQB
看了 已知圆C:(x-1)2+y2...的网友还看了以下:
已知直线l1:ax-by+k=0;l2:kx-y-1=0,其中a是常数,a≠0.(1)求直线l1和 2020-04-13 …
已知M(-3,0)﹑N(3,0),P为坐标平面上的动点,且直线PM与直线PN的斜率之积为常数m(m 2020-04-13 …
已知椭圆x224+y216=1,直线l:x12+y8=1.P是l上点,射线OP交椭圆于点R,又点Q 2020-04-13 …
关于造句的执着是———,————线上填诗句哦如执着是千磨万击还坚劲,任尔东西南北风!执着是———, 2020-05-14 …
中国近代,全国性金融中心不断迁移,基本轨迹是:上海→北京与天津→上海→重庆→上海。这反映出近代() 2020-05-17 …
下列个说法对吗?(1)点运动的轨迹是线;(2)线运动的轨迹一定是面;(3)面运动的轨迹一定是体. 2020-05-20 …
下列个说法对吗?(1)点运动的轨迹是线;(2)线运动的轨迹一定是面;(3)面运动的轨迹一定是体. 2020-05-20 …
“研究平抛物体的运动”实验中,A、B、C为平抛轨迹曲线上的三个点,AB、BC之间的水平距离均为S, 2020-05-21 …
迹线上的点的速度可以和迹线不相切么流线上每一点的速度都与该点处的切线平行,迹线是一个质点的轨迹线, 2020-06-19 …
椭圆准线的意义和性质抛物线准线的性质似乎容易懂,就是线上任意一点到定点和准线距离相等,那么椭圆有类 2020-06-21 …