早教吧作业答案频道 -->数学-->
已知△ABC的三边a,b,c满足b2+c2=5a2,BE,CF分别为边AC,AB上的中线,建立适当的平面直角坐标系探究BE与CF的位置关系.
题目详情
已知△ABC的三边a,b,c满足b2+c2=5a2,BE,CF分别为边AC,AB上的中线,建立适当的平面直角坐标系探究BE与CF的位置关系.
▼优质解答
答案和解析
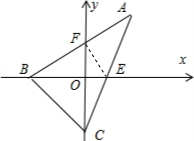 设BE、CF的交点为O,连接EF,则O点为△ABC的重心,
设BE、CF的交点为O,连接EF,则O点为△ABC的重心,
∴EF=
,OE=
,OF=
,
根据中线定理可知:BE2=
(2a2+2c2-b2),CF2=
(2a2+2b2-c2),
所以OE2+OF2=(
)2+(
)2=
(2a2+2c2-b2)+
(2a2+2b2-c2)=
(4a2+b2+c2)=
(4a2+5a2)=
a2=EF2
所以OE⊥OF,
即BE⊥CF,
所以以O为坐标原点,OE,OF分别为x,y轴,建立坐标系,可得BE⊥CF.
 设BE、CF的交点为O,连接EF,则O点为△ABC的重心,
设BE、CF的交点为O,连接EF,则O点为△ABC的重心,∴EF=
| a |
| 2 |
| BE |
| 3 |
| CF |
| 3 |
根据中线定理可知:BE2=
| 1 |
| 4 |
| 1 |
| 4 |
所以OE2+OF2=(
| BE |
| 3 |
| CF |
| 3 |
| 1 |
| 36 |
| 1 |
| 36 |
| 1 |
| 36 |
| 1 |
| 36 |
| 1 |
| 4 |
所以OE⊥OF,
即BE⊥CF,
所以以O为坐标原点,OE,OF分别为x,y轴,建立坐标系,可得BE⊥CF.
看了 已知△ABC的三边a,b,c...的网友还看了以下:
一道导数问题知道f'(x)=1/(1+x^2);求f(x)/(1+x^2)的导数要有过程,谢谢g( 2020-04-12 …
sql语句子查询中,无限子集,但是我想通过最上面的某一子集id,查询它下面的所有子集.如果说有1, 2020-04-27 …
求由方程f[0到y]e^(t^2)dt+f[0到x]costdt=0所确定的隐函数y=y(x)的导 2020-05-13 …
一道函数证明题..若函数f(x,y)对任意正实数t满足f(tx,ty)=f(x,y)乘以t的n次方 2020-05-13 …
若函数f(x,y)对任意正实数t满足f(tx,ty)=f(x,y)乘以t的n次方,就称f(x,y) 2020-05-13 …
抄写音标里的f时f是占上两格还是占三个格(三个格是手写体) 2020-05-16 …
已知f(x)之一原函数为sin3x,求∫f'(x)dx书上的答案是∫f'(x)dx=f(x)+Cf 2020-05-19 …
funny的音标是怎么划分的[ˈfʌni]的,是该读“发尼”还是“纺尼”呢?音标里的[ˈfʌni] 2020-06-21 …
定积分上下域为相反数,后面的f(x)需满足什么条件结果才为0啊?形式如下∫(-x,x)f(x)定积 2020-06-25 …
f(x+1)=x²6x+2,则f(x)=?f〔f(x)〕=4x+1,则f(x)=?主要要方法这是两 2020-06-27 …