早教吧作业答案频道 -->数学-->
己知:在等腰三角形ABC中,AB=AC,AD⊥BC于点D,以AC为边作等边三角形ACE,直线BE交直线AD于点F,连接FC.(1)如图1,120°<∠BAC<180°,△ACE与△ABC在直线AC的异侧,且FC交AE于点M.①求证:
题目详情
己知:在等腰三角形ABC中,AB=AC,AD⊥BC于点D,以AC为边作等边三角形ACE,直线BE交直线AD于点F,连接FC.
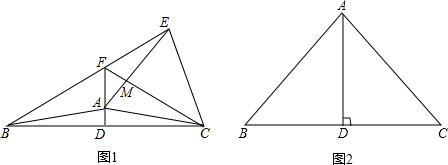
(1)如图1,120°<∠BAC<180°,△ACE与△ABC在直线AC的异侧,且FC交AE于点M.
①求证:∠FEA=∠FCA;
②猜想线段FE,FA,FD之间的数量关系,并证明你的结论:
(2)当60°<∠BAC<120°,且△ACE与△ABC在直线AC的同侧时,利用图2画出图形探究线段FE,FA,FD之间的数量关系,并直接写出你的结论.
(1)如图1,120°<∠BAC<180°,△ACE与△ABC在直线AC的异侧,且FC交AE于点M.
①求证:∠FEA=∠FCA;
②猜想线段FE,FA,FD之间的数量关系,并证明你的结论:
(2)当60°<∠BAC<120°,且△ACE与△ABC在直线AC的同侧时,利用图2画出图形探究线段FE,FA,FD之间的数量关系,并直接写出你的结论.

▼优质解答
答案和解析
(1)①∵AD⊥BC,AB=AC,
∴BD=DC,
∴FB=FC,
∴∠FBC=∠FCB,
∴AB=AC,
∴∠ABC=∠ACB,
∵∠FBA=∠FCA,
∵以AC为边作等边三角形ACE,
∴AE=AC=AB,
∴∠ABF=∠AEF,
∴∠ACF=∠AEF,
即:∠FEA=∠FCA;
②结论:EF=2FD-AF,
∵以AC为边作等边三角形ACE,
∴∠EAC=60°,
由①有,∠ACF=∠AEF,
∴∠EFC=∠EAC=60°,
由①得,BF=CF,FD⊥BC,
∴∠BFD=∠CFD,
∵∠BFD+∠CFD+∠EFC=180°,
∴∠BFD=∠CFD=
=60°,
∴∠FCD=90°-∠CFD=30°,
∴∠ACD+∠ACF=30°,
∴∠ECF=∠ECA-∠ACF=60°-∠ACF=60°-(30°-∠ACD)=30°+∠ACD,
如图1,
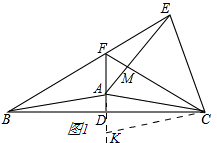
延长AD,在AD上截取AD=DK,连接CK,
∵AD⊥BC,
∴∠ACD=∠KCD,CA=CK
∴∠FCK=∠FCD+∠KCD=∠ACF+∠ACD+∠KCD=30°+∠KCD=30°+∠ACD,
∴∠FCK=∠ECF,
∵AC=CE,AC=CK,
∴CK=CE,
在△CFE和△CFK中,
,
∴△CFE≌△CFK,
∴FE=FK=FD+DK,
∵AD=DK,
∴FE=2FD-AF;
(2)②结论:EF=2FA-FD,
如图2,
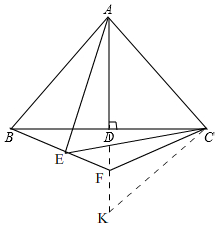
同(1)的方法得出∠FCK=∠ECF,
∵AC=CE,AC=CK,
∴CK=CE,
在△CFE和△CFK中,
,
∴△CFE≌△CFK,
∴FE=FK=FD+DK,
∵AD=DK,
∴FE=2FA-FD;
∴BD=DC,
∴FB=FC,
∴∠FBC=∠FCB,
∴AB=AC,
∴∠ABC=∠ACB,
∵∠FBA=∠FCA,
∵以AC为边作等边三角形ACE,
∴AE=AC=AB,
∴∠ABF=∠AEF,
∴∠ACF=∠AEF,
即:∠FEA=∠FCA;
②结论:EF=2FD-AF,
∵以AC为边作等边三角形ACE,
∴∠EAC=60°,
由①有,∠ACF=∠AEF,
∴∠EFC=∠EAC=60°,
由①得,BF=CF,FD⊥BC,
∴∠BFD=∠CFD,
∵∠BFD+∠CFD+∠EFC=180°,
∴∠BFD=∠CFD=
| 180°-∠EFC |
| 2 |
∴∠FCD=90°-∠CFD=30°,
∴∠ACD+∠ACF=30°,
∴∠ECF=∠ECA-∠ACF=60°-∠ACF=60°-(30°-∠ACD)=30°+∠ACD,
如图1,

延长AD,在AD上截取AD=DK,连接CK,
∵AD⊥BC,
∴∠ACD=∠KCD,CA=CK
∴∠FCK=∠FCD+∠KCD=∠ACF+∠ACD+∠KCD=30°+∠KCD=30°+∠ACD,
∴∠FCK=∠ECF,
∵AC=CE,AC=CK,
∴CK=CE,
在△CFE和△CFK中,
|
∴△CFE≌△CFK,
∴FE=FK=FD+DK,
∵AD=DK,
∴FE=2FD-AF;
(2)②结论:EF=2FA-FD,
如图2,

同(1)的方法得出∠FCK=∠ECF,
∵AC=CE,AC=CK,
∴CK=CE,
在△CFE和△CFK中,
|
∴△CFE≌△CFK,
∴FE=FK=FD+DK,
∵AD=DK,
∴FE=2FA-FD;
看了 己知:在等腰三角形ABC中,...的网友还看了以下:
1.请写出一个图像经过(1.1)的一次函数表达式下面还有2.点A为直线y=-2x+2上的一点,且点 2020-04-08 …
点A为直线y= - 2x+2上的一点,且点A到两坐标轴的距离相等,则点A的坐标为? 2020-05-16 …
高一物理问题(急)在线等质点A向东运动2M用了2S到质点B,质点B向北运动3M用了2S到质点C,质 2020-05-17 …
点P是矩形ABCD的边AD上的一个动点,矩形的两条边长AB、BC分别为8和15,求点P到矩形的两条 2020-05-20 …
1.一个有理数在数轴上的对应点为A,将A点先向右移动5个单位长度,再向左移动4个单位长度得到点B, 2020-06-27 …
如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交 2020-07-18 …
如图所示,以o为圆心的圆周上有六个等分点a、b、c、d、e、f.等量正、负点电荷分别放置在a、d两 2020-07-20 …
如图,数轴上线段MO(O为原点)的七等分点A.B.C.D.E.F中,只有两点对应的数是整数,点M对 2020-07-30 …
已知椭圆的焦距与短轴长相等,点A,B,C都在椭圆C上,且AB、AC分别过两个焦点F1、F2.(I) 2020-07-31 …
已知图中数轴上线段MO(O是原点)的七等分点A、B、C、D、E、F中,只有两点对应的数是整数,点M 2020-08-02 …