早教吧作业答案频道 -->数学-->
探究如图①,分别以△ABC的两边AB和AC为边向△ABC外作正三角形ABD和正三角形ACE,连结DC、BE,求证:DC=BE.拓展如图②,在四边形ABCD中,AB=BC=5,∠ABC=45°,连结AC、BD,若∠DAC=90°
题目详情
【探究】如图①,分别以△ABC的两边AB和AC为边向△ABC外作正三角形ABD和正三角形ACE,连结DC、BE,求证:DC=BE.
【拓展】如图②,在四边形ABCD中,AB=BC=5,∠ABC=45°,连结AC、BD,若∠DAC=90°,AC=AD,则BD的长为___.
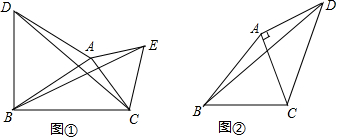
【拓展】如图②,在四边形ABCD中,AB=BC=5,∠ABC=45°,连结AC、BD,若∠DAC=90°,AC=AD,则BD的长为___.

▼优质解答
答案和解析
【探究】∵以AB、AC为边分别向外做等边△ABD和等边△ACE,
∴AD=AB,AE=AC,∠ACE=∠AEC=60°,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴CD=BE;
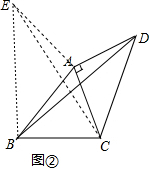
【拓展】如图②,以AB为边向外作等腰直角三角形AB,AE=AB,∠BAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ACE≌△ABD,
∴CE=BD,
∵BE=
AB=5
,
∵∠ABC=45°,
∴∠EBC=90°,
∴CE=
=5
,
∴BD=5
,
故答案为:5
.
∴AD=AB,AE=AC,∠ACE=∠AEC=60°,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
|

∴△DAC≌△BAE(SAS),
∴CD=BE;
【拓展】如图②,以AB为边向外作等腰直角三角形AB,AE=AB,∠BAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
|
∴△ACE≌△ABD,
∴CE=BD,
∵BE=
| 2 |
| 2 |
∵∠ABC=45°,
∴∠EBC=90°,
∴CE=
| BE2+BC2 |
| 3 |
∴BD=5
| 3 |
故答案为:5
| 3 |
看了 探究如图①,分别以△ABC的...的网友还看了以下:
比中交下列每组字母或单词的读音,相同的用S,不同的用D表示:b,d,c,e,c,a,b,c,a,e 2020-05-14 …
已知a+b+c=H a+b+e=J a+d+e=K b+c+d=M c+d+e=N 求a=?b=? 2020-05-16 …
设栈S的初始状态为空,元素a,b,c,d,e,f依次入栈S,出栈的序列为b,d,f,e,c,a…… 2020-05-17 …
设有关系模式R(A,B,C,D,E,F),若有如下的函数依赖集F={A→B,(C,A)→D, (E, 2020-05-24 …
给定关系模式R(A.B,C,D)、S(C,D,E),与语句如下:A.A.C. S.C B.A.,B, 2020-05-26 …
设实数a,b,c,d,e满足(a+c)(a+d)=(b+c)(b+d)=e≠O,且a≠b,那么(a 2020-06-08 …
如图是膝跳反射的示意图,请根据你所知道的回答第21~23小题:该反射的神经传导通路的顺序是()A. 2020-06-28 …
如图是膝跳反射的示意图,请根据你所知道的回答第37~40小题:该反射的神经传导通路的顺序是()A. 2020-06-28 …
关于java的swap比如有[a,b,c,d,e]5个字母...用swap交换为[d,e,c,a, 2020-07-17 …
一个9位数abcdefghi满足:1.a+b+...+h+i=cd2.a(b+d-c)=243.( 2020-07-19 …