早教吧作业答案频道 -->数学-->
已知AB是半圆O的直径,点C在半圆O上.(1)如图1,若AC=3,∠CAB=30°,求半圆O的半径;(2)如图2,M是BC的中点,E是直径AB上一点,AM分别交CE,BC于点F,D.过点F作FG∥AB交边BC于点G,若△ACE
题目详情
已知AB是半圆O的直径,点C在半圆O上.
(1)如图1,若AC=3,∠CAB=30°,求半圆O的半径;
(2)如图2,M是
的中点,E是直径AB上一点,AM分别交CE,BC于点F,D.过点F作FG∥AB交边BC于点G,若△ACE与△CEB相似,请探究以点D为圆心,GB长为半径的⊙D与直线AC的位置关系,并说明理由.
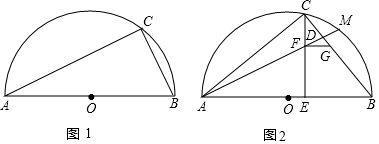
(1)如图1,若AC=3,∠CAB=30°,求半圆O的半径;
(2)如图2,M是
 |
| BC |

▼优质解答
答案和解析
(1)∵AB是半圆O的直径,
∴∠C=90°,
在Rt△ACB中,AB=
,
=
=2
,
∴OA=
;
(2)⊙D与直线AC相切.
理由如下:
由(1)得∠ACB=90°,
∵∠AEC=∠ECB+∠6,
∴∠AEC>∠ECB,∠AEC>∠6,
∵△ACE与△CEB相似,
∴∠AEC=∠CEB=90°,
在Rt△ACD,Rt△AEF中分别有
∠1+∠3=90°,∠2+∠4=90°,
∵M是
的中点,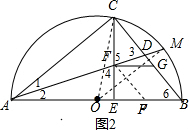
∴∠COM=∠BOM,
∴∠1=∠2,
∴∠3=∠4.
∵∠4=∠5,
∴∠3=∠5,
∴CF=CD,
过点F作FP∥GB交于AB于点P,则∠FPE=∠6,
在Rt△AEC,Rt△ACB中分别有
∠CAE+∠ACE=90°,∠CAE+∠6=90°,
∴∠ACE=∠6=∠FPE,
在△ACF与△APF中,
,
∴△ACF≌△APF,
∴CF=FP,
∵FP∥GB,FG∥AB,
∴四边形FPBG是平行四边形,
∴FP=GB,
∴CD=GB,
∵CD⊥AC,
∴点D到直线AC的距离为线段CD的长,
∴⊙D与直线AC相切.
∴∠C=90°,
在Rt△ACB中,AB=
| AC |
| cos∠CAB |
=
| 3 |
| cos30° |
=2
| 3 |
∴OA=
| 3 |
(2)⊙D与直线AC相切.
理由如下:
由(1)得∠ACB=90°,
∵∠AEC=∠ECB+∠6,
∴∠AEC>∠ECB,∠AEC>∠6,
∵△ACE与△CEB相似,
∴∠AEC=∠CEB=90°,
在Rt△ACD,Rt△AEF中分别有
∠1+∠3=90°,∠2+∠4=90°,
∵M是
 |
| BC |

∴∠COM=∠BOM,
∴∠1=∠2,
∴∠3=∠4.
∵∠4=∠5,
∴∠3=∠5,
∴CF=CD,
过点F作FP∥GB交于AB于点P,则∠FPE=∠6,
在Rt△AEC,Rt△ACB中分别有
∠CAE+∠ACE=90°,∠CAE+∠6=90°,
∴∠ACE=∠6=∠FPE,
在△ACF与△APF中,
|
∴△ACF≌△APF,
∴CF=FP,
∵FP∥GB,FG∥AB,
∴四边形FPBG是平行四边形,
∴FP=GB,
∴CD=GB,
∵CD⊥AC,
∴点D到直线AC的距离为线段CD的长,
∴⊙D与直线AC相切.
看了 已知AB是半圆O的直径,点C...的网友还看了以下:
已知,如图8,如图所示,正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以 2020-05-16 …
如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形 2020-05-16 …
如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形 2020-05-16 …
如图所示,正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正 2020-05-17 …
已知椭圆C:x2/a2+y2/b2=1(a>b>0)过点(1,2/3)且历心率e=1/2求椭圆方程 2020-06-15 …
(1/2)已知函数f(x)=ax^2+1(a>0),g(x)=x^3+bx.若曲线f(x)与曲线g 2020-06-27 …
如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形 2020-07-29 …
在同一直角坐标系中由抛物线y=x^-(5c-3)x-c和三个点G((-1/2)c,(5/2)c), 2020-07-30 …
已知椭圆C:x2a2+y2b2=1(a>b>0)的左焦点为F(-1,0),O为坐标原点,点G(1, 2020-07-31 …
已知椭圆C:x^2/a^2+y^2/b^2=1(a>b>0)过点(1,3/2),且离心率e=1/2( 2020-11-27 …