早教吧作业答案频道 -->数学-->
如图,△ABC是等腰直角三角形,AB=42,D为斜边BC上的一点(D与B、C均不重合),连结AD,把△ABD绕点A按逆时针旋转后得到△ACE,连结DE,设BD=x.(1)求证:∠DCE=90°;(2)当△DCE的面积为6
题目详情
如图,△ABC是等腰直角三角形,AB=4
,D为斜边BC上的一点(D与B、C均不重合),连结AD,把△ABD绕点A按逆时针旋转后得到△ACE,连结DE,设BD=x.
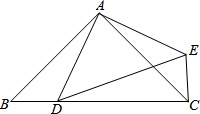
(1)求证:∠DCE=90°;
(2)当△DCE的面积为6时,求x的值;
(3)当D在斜边BC上运动时(D与B、C均不重合)四边形ADCE的面积S是否随着x的变化而变化?若变化,请求出S与x之间的函数关系式;若不变,求出S的值.
| 2 |

(1)求证:∠DCE=90°;
(2)当△DCE的面积为6时,求x的值;
(3)当D在斜边BC上运动时(D与B、C均不重合)四边形ADCE的面积S是否随着x的变化而变化?若变化,请求出S与x之间的函数关系式;若不变,求出S的值.
▼优质解答
答案和解析
(1)∵△ABD绕点A按逆时针旋转后得到△ACE,
∴△ACE≌△ABD,
∴∠ABD=∠ACE,
又∵△ABC是等腰直角三角形,且BC为斜边,
∴∠ABD+∠ACD=90°,
∴∠ACE+∠ACD=90°,
即:∠DCE=90°;
(2)∵AC=AB=4
,
∴BC2=AC2+AB2=(4
)2+(4
)2=64,
∴BC=8,
∵△ACE≌△ABD,∠DCE=90°,
∴CE=BD=x,而BC=8,
∴DC=8-x,
∴Rt△DCE的面积为:
DC•CE=
(8-x)x.
∴
(8-x)x=6,
即-x2+8x-12=0.
解得x=2或x=6;
(3)因为△ACE≌△ABD,
所以△ABD的面积等于△ACE的面积,
所以四边形ADCE的面积S不变,
S=
×4
×4
=16.
∴△ACE≌△ABD,
∴∠ABD=∠ACE,
又∵△ABC是等腰直角三角形,且BC为斜边,
∴∠ABD+∠ACD=90°,
∴∠ACE+∠ACD=90°,
即:∠DCE=90°;
(2)∵AC=AB=4
| 2 |
∴BC2=AC2+AB2=(4
| 2 |
| 2 |
∴BC=8,
∵△ACE≌△ABD,∠DCE=90°,
∴CE=BD=x,而BC=8,
∴DC=8-x,
∴Rt△DCE的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
即-x2+8x-12=0.
解得x=2或x=6;
(3)因为△ACE≌△ABD,
所以△ABD的面积等于△ACE的面积,
所以四边形ADCE的面积S不变,
S=
| 1 |
| 2 |
| 2 |
| 2 |
看了 如图,△ABC是等腰直角三角...的网友还看了以下:
下列各项中划线字注音全对的一项是A.晕圈(yùn)纵横决荡(hèng)外壳(ké)奇崛(jué)B 2020-05-14 …
如图所示.倾角为θ的斜面上有A、B、C三点,现从这三点分别以不同的初速度水平抛出一小球,三个小球均 2020-05-17 …
已知等边三角形abc的边长为4,点a的坐标为(-1,0)已知等边三角形ABC的边长为4点,点A的坐 2020-05-20 …
以等腰三角形ABC的斜边AB为边,作菱形ABDE,使D.E.C三点在同一直线上,求证角CAE=1/ 2020-06-17 …
已知a,b,c是△ABC的三边长,如果(c-5)2+|b-12|+a2−26a+169=0,则△A 2020-07-18 …
已知三边长为a,b,c,如果(a-5)+|b-12|+c-26c+169=0,则△ABC是().A 2020-07-18 …
已知a,b,c是三角形ABC的三边长,(a-5)^2+|b-12|+c^2-26c+169=0,则 2020-07-18 …
四边形OABC是矩形,OA=4,OC=8,将矩形OABC沿直线Ac折叠四边形OABC是矩形,OA= 2020-07-26 …
已知坐标平面内三点A(-1,1),B(1,1),C(2,√3+1)1)求直线AB,BC,AC的斜率 2020-07-31 …
如图所示,在A点静止的同一铁块沿AB、AC、AD三个光滑斜面下滑到斜面底端,则()A.沿AB滑下时动 2020-11-02 …