早教吧作业答案频道 -->数学-->
如图,分别以△ABC的边AB、AC为边向形外作正△ABD和正△ACE,且DF∥AE,EF∥AD.(1)当∠BAC满足什么条件时,四边形ADFE为矩形?(2)当∠BAC满足什么条件时,四边形ADFE不存在?(3)当△ABC
题目详情
如图,分别以△ABC的边AB、AC为边向形外作正△ABD和正△ACE,且DF∥AE,EF∥AD.
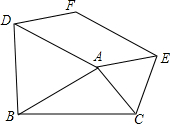
(1)当∠BAC满足什么条件时,四边形ADFE为矩形?
(2)当∠BAC满足什么条件时,四边形ADFE不存在?
(3)当△ABC满足什么条件时,四边形ADFE为菱形?
(4)当△ABC满足什么条件时,四边形ADFE为正方形?
(以上4小题,都不需说明理由)

(1)当∠BAC满足什么条件时,四边形ADFE为矩形?
(2)当∠BAC满足什么条件时,四边形ADFE不存在?
(3)当△ABC满足什么条件时,四边形ADFE为菱形?
(4)当△ABC满足什么条件时,四边形ADFE为正方形?
(以上4小题,都不需说明理由)
▼优质解答
答案和解析
∵DF∥AE,EF∥AD,
∴四边形ADFE是平行四边形,
∵△ABD与△ACE是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠EAC=60°,
(1)当∠BAC=150°时,
理由:∵∠DAE=360°-∠BAC-∠DAB-∠EAC=90°,
∴∠BAC=150°,四边形ADFE为矩形.
(2)当∠BAC=60°时,平行四边形ADFE不存在.
理由:∵∠DAE=∠DAB+∠BAC+∠EAC=60°+60°+60°=180°,
∴D,A,E共线,
∴平行四边形ADFE不存在.
(3)当AB=AC时,平行四边形ADFE是菱形.
理由:∵AD=AB,AE=AC,AB=AC,
∴AD=AE,
∵四边形ADFE是平行四边形,
∴平行四边形ADFE是菱形.
(3)AB=AC时,且∠BAC=150°,四边形ADFE为正方形.
理由:∵AD=AB,AE=AC,AB=AC,
∴AD=AE,
∵四边形ADFE是平行四边形,
∴平行四边形ADFE是菱形.
∵∠BAC=150°,
∴∠DAE=90°,
∴四边形ADFE为正方形.
∴四边形ADFE是平行四边形,
∵△ABD与△ACE是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠EAC=60°,
(1)当∠BAC=150°时,
理由:∵∠DAE=360°-∠BAC-∠DAB-∠EAC=90°,
∴∠BAC=150°,四边形ADFE为矩形.
(2)当∠BAC=60°时,平行四边形ADFE不存在.
理由:∵∠DAE=∠DAB+∠BAC+∠EAC=60°+60°+60°=180°,
∴D,A,E共线,
∴平行四边形ADFE不存在.
(3)当AB=AC时,平行四边形ADFE是菱形.
理由:∵AD=AB,AE=AC,AB=AC,
∴AD=AE,
∵四边形ADFE是平行四边形,
∴平行四边形ADFE是菱形.
(3)AB=AC时,且∠BAC=150°,四边形ADFE为正方形.
理由:∵AD=AB,AE=AC,AB=AC,
∴AD=AE,
∵四边形ADFE是平行四边形,
∴平行四边形ADFE是菱形.
∵∠BAC=150°,
∴∠DAE=90°,
∴四边形ADFE为正方形.
看了 如图,分别以△ABC的边AB...的网友还看了以下:
如图,把两条足够长的等宽的纸带交叉放置(不重合),重叠部分形成四边形ABCD,则四边形ABCD是( 2020-05-17 …
判断下列命题是否正确,并说明理由.(矩形的判定)1、对角互补的平行四边形是矩形.2、一组邻角相等的 2020-05-20 …
从四边形内找一点,使该点到各边的距离都相等的图形是()A.平行四边形,矩形,菱形B.菱形,矩形,正 2020-07-30 …
下列说法正确的是:A对顶角互相垂直的四边形是菱角B有一个角是直角的平行四边形是矩形C有一个角是直角 2020-08-01 …
(8分)若矩形的一个短边与长边的比值为,(黄金分割数),我们把这样的矩形叫做黄金矩形(1)操作:请 2020-08-02 …
若矩形的一个短边与长边的比值为,(黄金分割数),我们把这样的矩形叫做黄金矩形。(1)操作:请你在如 2020-08-02 …
(2005•扬州)若一个矩形的短边与长边的比值为(黄金分割数),我们把这样的矩形叫做黄金矩形.(1 2020-08-02 …
若一个矩形的短边与长边的比值为(黄金分割数),我们把这样的矩形叫做黄金矩形.(1)操作:请你在如图 2020-08-02 …
下列说法错误的是a对角线互相平分的四边形是平行四边形b对角线互相垂直的四边形是矩形c对角线相等的平行 2020-10-31 …
(2011•绵阳)下列关于矩形的说法,正确的是()A.对角线相等的四边形是矩形B.对角线互相平分的四 2020-11-12 …