早教吧作业答案频道 -->数学-->
已知:如图,在△ABC中,BC=BA,BE平分∠CBA交边CA于点E,∠ABC=45°,CD⊥AB,垂足为D,F为BC中点,BE与DF、DC分别交于点G、H.(1)求证:BH=CA;(2)求证:BG2=GE2+EA2.
题目详情
已知:如图,在△ABC中,BC=BA,BE平分∠CBA交边CA于点E,∠ABC=45°,CD⊥AB,垂足为D,F为BC中点,BE与DF、DC分别交于点G、H.
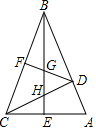
(1)求证:BH=CA;
(2)求证:BG2=GE2+EA2.

(1)求证:BH=CA;
(2)求证:BG2=GE2+EA2.
▼优质解答
答案和解析
(1)∵BC=BA,BE平分∠CBA,
∴BH⊥CA,
∴∠BEA=90°,
又CD⊥AB,∠ABC=45°,
∴∠BDC=∠CDA=90°,
∴∠BCD=∠ABC=45°,∠BAC+∠DCA=90°,∠BAC+∠ABE=90°,
∴DB=DC,∠ABE=∠DCA.
∵在△DBH与△DCA中,
∵
,
∴△DBH≌△DCA(AAS),
∴BH=AC;
(2)如图,连接CG.
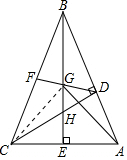
∵AB=BC,BE⊥AC,
∴BE垂直平分AC,
∴AG=CG.
又∵F点是BC的中点,DB=DC,
∴DF垂直平分BC,
∴BG=CG,
∴AG=BG,BG2=GE2+EA2.
在Rt△AGE中,∵AG2=GE2+EA2,
∴BG2=GE2+EA2.
∴BH⊥CA,
∴∠BEA=90°,
又CD⊥AB,∠ABC=45°,
∴∠BDC=∠CDA=90°,
∴∠BCD=∠ABC=45°,∠BAC+∠DCA=90°,∠BAC+∠ABE=90°,
∴DB=DC,∠ABE=∠DCA.
∵在△DBH与△DCA中,
∵
|
∴△DBH≌△DCA(AAS),
∴BH=AC;
(2)如图,连接CG.

∵AB=BC,BE⊥AC,
∴BE垂直平分AC,
∴AG=CG.
又∵F点是BC的中点,DB=DC,
∴DF垂直平分BC,
∴BG=CG,
∴AG=BG,BG2=GE2+EA2.
在Rt△AGE中,∵AG2=GE2+EA2,
∴BG2=GE2+EA2.
看了 已知:如图,在△ABC中,B...的网友还看了以下:
下列符号代表精子的染色体组成 a与a'是一对同源染色体 其余以此类推 下列哪四个精子来自同一个精原 2020-05-17 …
下列符号代表精子的染色体组成 a与a'是一对同源染色体 其余以此类推 下列哪四个精子来自同一个精原 2020-05-17 …
可逆反应各物质起始量比=系数比,那么反应过程中物质的量比还等于系数比吗比如aA+bB=cC+dD, 2020-05-23 …
已知x>0,y>0,a=x+y,b=根号下x2+xy+y2,c=m根号下xy问是否存在正数使得对于 2020-06-12 …
求因式分解的答案:1.x^4-11x^2y^2+y^22.x^4-12x+3233.a^3+b^3 2020-06-27 …
已知ΔABC的内角A.B.C满足sin2A+sin(A-B已知ΔABC的内角A.B.C满足sin2 2020-06-27 …
A=BC若C可逆,则A与B秩相等吗?A、B、C都为同规格矩阵 2020-06-30 …
已知a,b,c(a<b<c)成等差数列,将其中两个数交换,得到的三个数依次成等比数列,则(a²+c 2020-07-28 …
已知△ABC的一边BC在平面α内,△A'BC为△ABC在平面α内的射影,则∠BAC与∠BA'C的大 2020-07-30 …
如何将逻辑函数表达式成为最简与或式?请高手帮忙解答下面四道题,谢谢啦!着急啊!1、F=AB+ABD+ 2020-11-01 …