早教吧作业答案频道 -->数学-->
如图,抛物线y=-x2+5x+n经过点A(1,0),与y轴交于点B.(1)求抛物线的解析式;(2)P是y轴上一点,且△PAB是以AB为腰的等腰三角形,试求P点坐标.(3)将抛物线y=-x2+5x+n沿着坐标轴方向经
题目详情
如图,抛物线y=-x2+5x+n经过点A(1,0),与y轴交于点B.
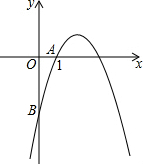
(1)求抛物线的解析式;
(2)P是y轴上一点,且△PAB是以AB为腰的等腰三角形,试求P点坐标.
(3)将抛物线y=-x2+5x+n沿着坐标轴方向经过怎样的一次平移可以使它使它经过原点.

(1)求抛物线的解析式;
(2)P是y轴上一点,且△PAB是以AB为腰的等腰三角形,试求P点坐标.
(3)将抛物线y=-x2+5x+n沿着坐标轴方向经过怎样的一次平移可以使它使它经过原点.
▼优质解答
答案和解析
(1)∵抛物线y=-x2+5x+n经过点A(1,0)
∴n=-4
∴y=-x2+5x-4;
(2)∵抛物线的解析式为y=-x2+5x-4,
∴令x=0,则y=-4,
∴B点坐标(0,-4),AB=
,
①当PA=AB时,PA=AB,则有OB=OP
此时P(0,4)
②当PB=AB时,|PB|=
,
故P(0,
-4);P(0,-
-4)
因此P点的坐标为P(0,4);P(0,
-4);P(0,-
-4);
(3)将抛物线y=-x2+5x-4沿着坐标轴方向向左平移1个,或向左平移4个,或向上平移4个均平移可以使它使它经过原点.
∴n=-4
∴y=-x2+5x-4;
(2)∵抛物线的解析式为y=-x2+5x-4,
∴令x=0,则y=-4,
∴B点坐标(0,-4),AB=
| 17 |
①当PA=AB时,PA=AB,则有OB=OP
此时P(0,4)
②当PB=AB时,|PB|=
| 17 |
故P(0,
| 17 |
| 17 |
因此P点的坐标为P(0,4);P(0,
| 17 |
| 17 |
(3)将抛物线y=-x2+5x-4沿着坐标轴方向向左平移1个,或向左平移4个,或向上平移4个均平移可以使它使它经过原点.
看了 如图,抛物线y=-x2+5x...的网友还看了以下:
如图,是一些物体的质量表.一枚大头针的质量是氢原子质量的倍.地球的质量是成人质量的倍.质量是60k 2020-04-09 …
任何一个运动着的物体,小到电子、质子,大到行星、太阳,都有一种波与之对应,波长λ=h/p,式中h为 2020-04-26 …
自然界中,凡是有的物体都叫生物。生物具有一些基本特征,这些生物特征包括:、生长、和等。 2020-05-13 …
质量是2kg的物体放在水平上,受到6N的水平拉力后,物体由静止开始运动,10S末的速度为8m/s. 2020-05-13 …
为什么运动着的物体质量比静止时候要大谢谢了,从相对论讲 2020-05-14 …
在水里浮着的物体受到水的浮力,而在水里下沉的物体没有受到水的浮力,对错? 2020-05-16 …
运动着的物体受到的力与运动方向相反时,物体运动状态改变表现为我们老师说是减速,但我认为还有匀速运动 2020-05-16 …
在水平地面上放一个重力是50N的物体,用2N的水平拉力,使物体在水平面上作匀速直线运动,则物体受到 2020-05-17 …
圆周运动.有一个粗糙木板,可以绕着中间固定的轴匀速转动.在木板上放一个上下底面接触放置、总质量是M 2020-05-17 …
物体的动能与物体的质量成正比这句话为什么是错的?物体的动能与物体的质量成正比物体的动能与物体的速度 2020-05-23 …