早教吧作业答案频道 -->数学-->
如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).(Ⅰ)若y1•y2=-8,求抛物线C的方程;(Ⅱ)若直线AF与x轴不垂直,直
题目详情
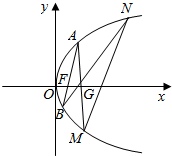
如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).
(Ⅰ)若y1•y2=-8,求抛物线C的方程;
(Ⅱ)若直线AF与x轴不垂直,直线AF交抛物线C于另一点B,直线BG交抛物线C于另一点N.求证:直线AB与直线MN斜率之比为定值.

(Ⅰ)若y1•y2=-8,求抛物线C的方程;
(Ⅱ)若直线AF与x轴不垂直,直线AF交抛物线C于另一点B,直线BG交抛物线C于另一点N.求证:直线AB与直线MN斜率之比为定值.
▼优质解答
答案和解析
(Ⅰ) 设直线AM的方程为x=my+p,代入y2=2px得y2-2mpy-2p2=0,
∴y1•y2=-2p2=-8,
∴p=2,
∴抛物线C:y2=4x;
(Ⅱ)证明设B(x3,y3),N(x4,y4),则y3•y4=-2p2,y1•y3=-p2,
∴直线AB与直线MN斜率之比为
=
=
=2.
∴y1•y2=-2p2=-8,
∴p=2,
∴抛物线C:y2=4x;
(Ⅱ)证明设B(x3,y3),N(x4,y4),则y3•y4=-2p2,y1•y3=-p2,
∴直线AB与直线MN斜率之比为
| ||
|
| y2+y4 |
| y1+y3 |
| ||
| y1+y3 |
看了 如图,已知抛物线C:y2=2...的网友还看了以下:
能判定△ABC与△A'B'C'相似的条件是( )A.A'B'分之AB=A'C'分之AC B. 2020-05-16 …
分解因式(a-b-c)(a+b-c)-(b-c-a)(b+c-a)正确答案是这个:(a+b-c)( 2020-05-17 …
有难度M{A,B,C}==(A+B+C)/3m{A,B,C}=A(A为三数中最小的一个)则若M{A 2020-06-13 …
a(b-c)^5+b(c-a)^5+c(a-b)^5分解为(a-b)(b-c)(c-a)L(aa( 2020-07-09 …
求证:A∩(B∪C)=(A∪B)∩(A∪C)(1)假设x∈A∩(B∪C),则x∈A且x∈B∪C,所 2020-07-20 …
设a,b,c都是正数且a+b+c=1,求证:(1+a)(1+b)(1+c)≥8(1-a)(1-b) 2020-07-25 …
有三个数a,b,c,其中满足a+b>c,b+c>a,a+c>b,结果是有三个数a,b,c,其中满足a 2020-11-01 …
在三角形ABC和三角形A'B'C'中CD,C'D'分别是高,并且AC=A'C;,CD=C'D',∠A 2020-11-28 …
已知a+b+c=0,abc不等于0,且a,b,c,互不相等,求证:[(b-c)/a+(c-a)/b+ 2020-12-01 …
已知a+b+c=0,abc不等于0,且a,b,c,互不相等,求证:[(b-c)/a+(c-a)/b+ 2020-12-01 …