早教吧作业答案频道 -->数学-->
如图,A(0,6),B(-6,0),点C、D同时从点O、A出发以每秒1个单位的速度分别沿着x轴正半轴和射线AO方向运动,同时点E从点B出发,以每秒2个单位沿着射线BO运动,过点C的直线l⊥x轴,点F
题目详情
如图,A(0,6),B(-6,0),点C、D同时从点O、A出发以每秒1个单位的速度分别沿着x轴正半轴和射线AO方向运动,同时点E从点B出发,以每秒2个单位沿着射线BO运动,过点C的直线l⊥x轴,点F是直线l在x轴上方的一点,且EF=ED,以DE和EF为邻边作菱形DEFG;当点C和点E重合时各点同时停止运动;直线m:y=2x+2交x轴于点M,交y轴于点N;设运动时间为t.
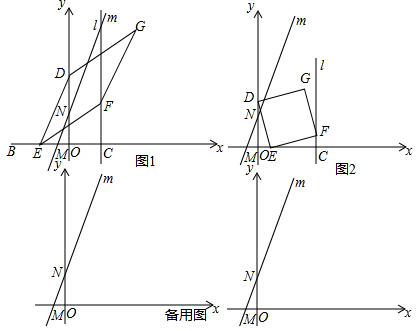
(1)如图1直接写出点M和点N的坐标并用t的代数式表示CE和OD的长度.
M___,N___,CE=___,OD=___.
(2)如图2,当点E在线段OC之间时,证明:菱形DEFG为正方形.
(3)在整个运动过程中,
①当t的值为多少时,四边形DEFG有一个顶点落在直线m上;
②记点D关于直线m的对称点为点D′,当点D′恰好落在直线l上时,直接写出t的值是___.

(1)如图1直接写出点M和点N的坐标并用t的代数式表示CE和OD的长度.
M___,N___,CE=___,OD=___.
(2)如图2,当点E在线段OC之间时,证明:菱形DEFG为正方形.
(3)在整个运动过程中,
①当t的值为多少时,四边形DEFG有一个顶点落在直线m上;
②记点D关于直线m的对称点为点D′,当点D′恰好落在直线l上时,直接写出t的值是___.
▼优质解答
答案和解析
(1)∵y=2x+2交x轴于点M,交y轴于点N,
∴M(-1,0),N(0,2),
由题意,OE=t,AD=t,BE=2t,
∴EC=OB+OC-BE=6+t-2t=6-t,OD=OA-AD=6-t,
故答案为(-1,0),(0,2),6-t,6-t,
(2)证明:点E在线段OC之间
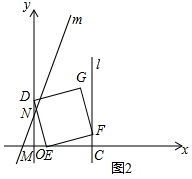
∵CE=6-t=OD,EF=ED,∠DOE=∠ECF=90°.
∴△DOE≌△ECF
∴∠DEO=∠EFC
∴∠DEO+∠CEF=∠EFC+∠CEF=90°,
∴∠DEF=90°
∴菱形DEFG是正方形.
(3)①当点D落在直线m上;即点D与点N重合,
可得6-t=2
∴t=4.
当点E落在直线m上;即点E与点M重合,
可得2t=5
∴t=2.5.
当点F落在直线m上;如图3,
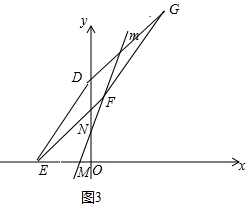
由△DOE≌△FCE
可得CF=OE=6-2t
把F ( t,6-2t )代入y=2x+2
6-2t=2t+2
∴t=1.
当点G落在直线m上;如图4,
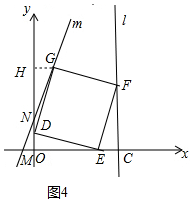
过G作GH⊥x轴于点H
容易证明△DOE≌△GHD;
∴GH=OD=6-t,HD=OE=2t-6
∴OH=HD+OD=t
把G (6-t,t )代入y=2x+2
t=2(6-t)+2∴t=
.
∴当t取4,2.5,1,
时,四边形DEFG有一个顶点落在直线m上
②如图5中,设DD′交直线m于F,作FG⊥OA于G.
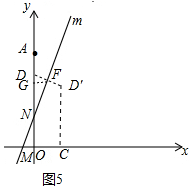
由题意,D关于直线m的对称点为点D′,当点D′恰好落在直线l上,
∴FG=
,AD=t,
由△DFG∽△FNG∽△MNO,
∴
=
=
=
,
∴DG=
t,GN=t,
∵GN=AN-AD-DG,
∴t=4-t-
t,
∴t=
.
∴t=
时,D关于直线m的对称点为点D′,当点D′恰好落在直线l上.
∴M(-1,0),N(0,2),
由题意,OE=t,AD=t,BE=2t,
∴EC=OB+OC-BE=6+t-2t=6-t,OD=OA-AD=6-t,
故答案为(-1,0),(0,2),6-t,6-t,
(2)证明:点E在线段OC之间

∵CE=6-t=OD,EF=ED,∠DOE=∠ECF=90°.
∴△DOE≌△ECF
∴∠DEO=∠EFC
∴∠DEO+∠CEF=∠EFC+∠CEF=90°,
∴∠DEF=90°
∴菱形DEFG是正方形.
(3)①当点D落在直线m上;即点D与点N重合,
可得6-t=2
∴t=4.
当点E落在直线m上;即点E与点M重合,
可得2t=5
∴t=2.5.
当点F落在直线m上;如图3,

由△DOE≌△FCE
可得CF=OE=6-2t
把F ( t,6-2t )代入y=2x+2
6-2t=2t+2
∴t=1.
当点G落在直线m上;如图4,

过G作GH⊥x轴于点H
容易证明△DOE≌△GHD;
∴GH=OD=6-t,HD=OE=2t-6
∴OH=HD+OD=t
把G (6-t,t )代入y=2x+2
t=2(6-t)+2∴t=
| 14 |
| 3 |
∴当t取4,2.5,1,
| 14 |
| 3 |
②如图5中,设DD′交直线m于F,作FG⊥OA于G.

由题意,D关于直线m的对称点为点D′,当点D′恰好落在直线l上,
∴FG=
| t |
| 2 |
由△DFG∽△FNG∽△MNO,
∴
| DG |
| FG |
| FG |
| GN |
| OM |
| ON |
| 1 |
| 2 |
∴DG=
| 1 |
| 4 |
∵GN=AN-AD-DG,
∴t=4-t-
| 1 |
| 4 |
∴t=
| 16 |
| 9 |
∴t=
| 16 |
| 9 |
看了 如图,A(0,6),B(-6...的网友还看了以下:
边缘粗糙,半径不同的两个轮子,作无滑动的摩擦传动.AB是大轮O上的两点,OA=R=0.8m,OB= 2020-05-13 …
1.编写程序计算电费:每月用电不超过50度,每度0.72元;超过50度时,超出部分每度1.20元. 2020-05-13 …
取标示量为2mg的奋乃静片10片,按药典规定检查含量均匀度.分别将每片配成50ml溶液,再将此溶液 2020-06-08 …
抛物线y=x2+bx+c经过A(0,2),B(3,2)两点,若两动点D、E同时从原点O分别沿着x轴 2020-06-11 …
点A、B、O分别以5个单位/s,2单位/s,1单位/s的速度向右移运动,几秒后,o点恰好成为线段中 2020-06-15 …
两名运动员在长30米的游泳池里来回游泳.甲的速度每秒1米,乙的速度每秒0.6米.他们同时分别在两名 2020-06-23 …
等腰直角△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线 2020-07-21 …
高数问题设函数f(x,y)在点(0,0)的某领域有定义,且fx(o,o)=3,fy(0,0)=-1, 2020-11-01 …
线性代数问题A*B=0和A*B=o(o表示0矩阵)到底有什么区别? 2020-11-06 …
某市为合理用电,鼓励各用户安装“峰谷”电表.该市原电价为每度0.53元,改装新电表后.每天晚上10点 2020-12-27 …