等腰直角△ABC和⊙O如图放置，已知AB=BC=1，∠ABC=90°，⊙O的半径为1，圆心O与直线AB的距离为5．现△ABC以每秒2个单位的速度向右移动，同时△ABC的边长AB、BC又以每秒0.5个

Question

等腰直角△ABC和⊙O如图放置，已知AB=BC=1，∠ABC=90°，⊙O的半径为1，圆心O与直线AB的距离为5．现△ABC以每秒2个单位的速度向右移动，同时△ABC的边长AB、BC又以每秒0.5个单位沿BA、BC方向增大．

⑴ 当△ABC的边(BC边除外)与圆第一次相切时，点B移动了多少距离？

⑵ 若在△ABC移动的同时，⊙O也以每秒1个单位的速度向右移动，则△ABC从开始移动，到它的边与圆最后一次相切，一共经过了多少时间？

⑶ 在⑵的条件下，是否存在某一时刻，△ABC各边刚好与⊙O都相切？若存在，求出刚好符合条件时两个图形移动了多少时间？若不存在，能否改变AB、BC沿BA、BC方向的速度，使△ABC各边刚好与⊙O都相切．

Answer 1

⑴ ，⑵6秒，（3）若圆能在△ABC的内部时，则存在，4秒；若圆O不能在三角形的内部，则不存在，t=

解析:由切线长定理可知C ^’ E= C ^’ D，设C ^’ D=x，则C ^’ E=x，易知C ^’ F= x

∴ x＋x=1   ∴x= －1  ∴CC ^’ =5－1－( －1)=5－     2分

∴点C运动的时间为                 3分

∴点B运动的的距离为                   4分

⑵设一共经过了t秒，根据题意得：2t-5=t+1

t =6

答：一共经过了6秒                 6分

⑶∵△ABC与⊙O从开始运动到第二次相切时，2t+1=t+5    t=4         7分

∴从开始运动到第二次相切的时间为4秒， 此时△ABC移至△A ^” B ^” C ^” 处，

A ^” B ^” =1＋4× =3                                             8分

连接B ^” O并延长交A ^” C ^” 于点P，则B ^” P⊥A ^” C ^” ，

且OP= ＜1        ∴此时⊙O与A ^” C ^” 相交           

∴不存在△ABC各边与⊙O都相切．                               9分

设AB、BC沿BA、BC方向的速度为t 则（1+4t）× =1        10分

t=                   11分

 

 

 

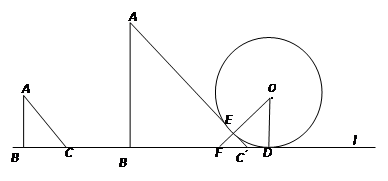
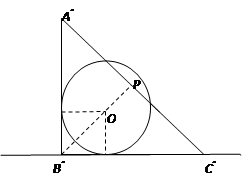
（1）当△ABC第一次与圆相切时，应是AC与圆相切．如图，△ABC移至△A′B′C′处，A′C′与⊙O切于点E，连OE并延长，交B′C′′于F．设⊙O与直线l切于点D，连OD，则OE⊥A′C′，OD⊥直线l．由切线长定理，以及直角三角形的性质可求得CD的值，进而求得CC′的值，从而求得点C运动的时间，也就有了点运动的时间，点B移动的距离也就可求得了．

（2）△ABC与⊙O从开始运动到最后一次相切时，应为AB与圆相切，路程差为6，速度差为1，故从开始运动到最后一次相切的时间为6秒．

（3）若圆能在△ABC的内部时，则存在；若圆O不能在三角形的内部，则不存在；即求在（2）条件下，AC与圆的位置关系即可．