早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax-3a与x轴交于A、B两点,与y轴交于点C,BO=CO.(1)求抛物线的解析式;(2)点P是第一象限抛物线上的一动点,连接AP,交y轴于点D,
题目详情
如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax-3a与x轴交于A、B两点,与y轴交于点C,BO=CO.
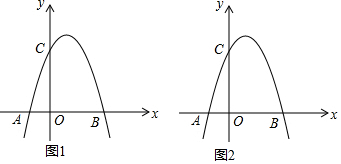
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的一动点,连接AP,交y轴于点D,连接CP,设P点横坐标为t,△CDP的面积为S,求S与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,过点P作PE⊥x轴于点E,连接PB,过点A作AF⊥PB于点F,交线段PE于点G,若点H在x轴负半轴上,PH=2GE,点M(0,m)在y轴正半轴上,连接PM、PH,∠HPM=2∠BHP,PH=2PM,求m的值.

(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的一动点,连接AP,交y轴于点D,连接CP,设P点横坐标为t,△CDP的面积为S,求S与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,过点P作PE⊥x轴于点E,连接PB,过点A作AF⊥PB于点F,交线段PE于点G,若点H在x轴负半轴上,PH=2GE,点M(0,m)在y轴正半轴上,连接PM、PH,∠HPM=2∠BHP,PH=2PM,求m的值.
▼优质解答
答案和解析
(1)当ax2-2ax-3a=0时,解得x=3或-1,
∴A(-1,0),B(3,0),
∴OA=1,OB=3,
∴OC=OB=3,
∴-3a=3,
∴a=-1,
∴y=-x2+2x+3.
(2)如图1中,作PE⊥x轴于E,PK⊥y轴于K.
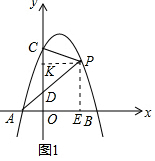
∵点P在第一象限,横坐标为t,
∴P(t,-t2+2t+3),
∵∠PKO=∠COB=∠PEO=90°,
∴四边形KPEO是矩形,
∴PK=OE=t,PE=OK,
∴PE=-t2+2t+3,AE=t+1,
∵∠PAE=∠DAO,
∴tan∠PAE=tan∠DAO,
∴
=
,
∴
=
,
∴OD=3-t,
∴CD=3-OD=t,
∴S=
PK•CD=
t2.
(3)设PH交y轴于点N.
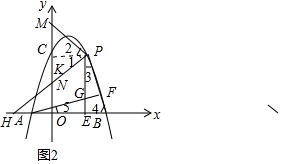
∵∠PKO=∠PKM=∠HON=90°,
∴PK∥x轴,
∴∠1=∠PHB,
∵∠MPH=2∠PHB,
∴MPH=2∠1,即∠1=∠2,
∵∠PKM=∠PKN,PK=PK,
∴△PKM≌△PKN,
∴PM=PN,MK=NK,
∵PH=2PM,
∴PN=HN,
∵∠HON=∠PKN,∠1=∠BHP,
∴△HON≌△PKN,
∴PK=HO,KN=ON,
∵AF⊥PB,
∴∠AFB=90°,
∴∠3+∠4=90°,
∵∠PEB=90°,
∴∠4+∠5=90°,
∴∠3=∠5,
∴tan∠3=tan∠5,
∴
=
,∵BE=OB-OE=3-t,
∴
=
,
∴GE=1,
∴OH=2EG=2,
∴PK=2,PE=3,
∴OK=3=OC,
∴点K与点C重合,
∴KN=
,
∴OM=3KN=
,即m=
∴A(-1,0),B(3,0),
∴OA=1,OB=3,
∴OC=OB=3,
∴-3a=3,
∴a=-1,
∴y=-x2+2x+3.
(2)如图1中,作PE⊥x轴于E,PK⊥y轴于K.

∵点P在第一象限,横坐标为t,
∴P(t,-t2+2t+3),
∵∠PKO=∠COB=∠PEO=90°,
∴四边形KPEO是矩形,
∴PK=OE=t,PE=OK,
∴PE=-t2+2t+3,AE=t+1,
∵∠PAE=∠DAO,
∴tan∠PAE=tan∠DAO,
∴
| PE |
| AE |
| DO |
| AO |
∴
| -t2+2t+3 |
| t+1 |
| OD |
| 1 |
∴OD=3-t,
∴CD=3-OD=t,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
(3)设PH交y轴于点N.

∵∠PKO=∠PKM=∠HON=90°,
∴PK∥x轴,
∴∠1=∠PHB,
∵∠MPH=2∠PHB,
∴MPH=2∠1,即∠1=∠2,
∵∠PKM=∠PKN,PK=PK,
∴△PKM≌△PKN,
∴PM=PN,MK=NK,
∵PH=2PM,
∴PN=HN,
∵∠HON=∠PKN,∠1=∠BHP,
∴△HON≌△PKN,
∴PK=HO,KN=ON,
∵AF⊥PB,
∴∠AFB=90°,
∴∠3+∠4=90°,
∵∠PEB=90°,
∴∠4+∠5=90°,
∴∠3=∠5,
∴tan∠3=tan∠5,
∴
| GE |
| AE |
| BE |
| PE |
∴
| GE |
| t+1 |
| 3-t |
| -t2+2t+3 |
∴GE=1,
∴OH=2EG=2,
∴PK=2,PE=3,
∴OK=3=OC,
∴点K与点C重合,
∴KN=
| 3 |
| 2 |
∴OM=3KN=
| 9 |
| 2 |
| 9 |
| 2 |
看了 如图,在平面直角坐标系中,O...的网友还看了以下:
看经纬度计算实际距离最近遇到一些地理题总是看经纬度计算距离的,如果是两点在同一条经线或纬线上就容易 2020-05-14 …
积分区域边界(不是内部)上含有奇点时,高斯公式是否可以直接使用OK,如果不可用,请问如何解这种题, 2020-05-17 …
双曲线上任意一点所成角的角平分线是否是该点在双曲线上的切线!如双曲线的焦点F1F2和双曲线上任意一 2020-06-16 …
点在直线上,点在直线外要怎么理解这句话啊?点在直线上就是直线是由点组成的而点在直线外根据直线它是向 2020-06-17 …
P是△ABC所在平面外的一点,O是P点在平面上的射影,若P点到△ABC三边距离相等,则O是△ABC 2020-07-16 …
在平面几何里有射影定理:设三角形ABC的两边AB垂直与AC.D是A点在BC边上的射影,则AB的平方 2020-07-30 …
已知P是焦点在x轴上的椭圆C上一点,点P到两焦点F1、F2的距离分别为4根号3和2根号3,角F1P 2020-07-31 …
下列命题中,正确的是①顶点在圆周上的角是圆周角;②圆内接四边形的对角不一定互补;③90°的圆周角所 2020-08-01 …
如图所示,在M点分别以不同的速度将两小球水平抛出,两小球分别落在水平地面上的P点、Q点.已知O点是M 2020-11-11 …
(2014•南昌模拟)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影,M为PD上一点, 2021-01-02 …