①若点A、B、C在数轴上分别表示-1、4、c，且点C到点A、B的距离之和是7，则c=；②关于x的方程|x-m|+|x-n|=k（m>n，k>0），借助数轴探究方程的解的情况，直接写出结论．

Question

①若点A、B、C在数轴上分别表示-1、4、c，且点C到点A、B的距离之和是7，则c=___；
②关于x的方程|x-m|+|x-n|=k（m>n，k>0），借助数轴探究方程的解的情况，直接写出结论．

Answer 1

①∵点A、B在数轴上分别表示-1、4，
∴AB=5，
∵点C到点A、B的距离之和是7，
∴C不可能在A、B之间，
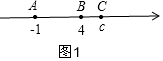
分两种情况：i）当C在B的右侧时，如图1，有AC+BC=7，
则c+1+c-4=7，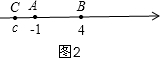
c=5；
ii）当C在A的左侧时，如图2，有AC+BC=7，
则-1-c+4-c=7，
c=-2，
综上所述，c的值为5或-2；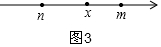
故答案为：5或-2；
②由题意可知：|x-m|+|x-n|的最小值为|m-n|=m-n，
当0当k=m-n时，原方程的解为：n≤x≤m，如图3，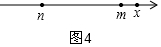
当k>m-n时，分两种情况：i）当x>m时，如图4，x-m+x-n=k，
2x=k+m+n，
x=(1)/(2)（k+m+n），
ii）当x<n时，如图5，m-x+n-x=k，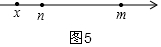
2x=m+n-k，
x=(1)/(2)（m+n-k），
此时原方程的解为：x₁=(1)/(2)（k+m+n），x₂=(1)/(2)（m+n-k）．