早教吧作业答案频道 -->数学-->
如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.(1)求证:BE=AD;(2)用含α的式子表示∠AMB的度数;(3)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,
题目详情
如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.
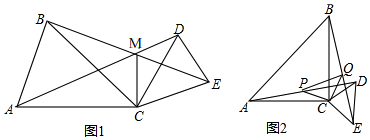
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

▼优质解答
答案和解析
(1)如图1,∵∠ACB=∠DCE=α,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴BE=AD;
(2)如图1,∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∵△ABC中,∠BAC+∠ABC=180°-α,
∴∠BAM+∠ABM=180°-α,
∴△ABM中,∠AMB=180°-(180°-α)=α;
(3)△CPQ为等腰直角三角形.
证明:如图2,由(1)可得,BE=AD,
∵AD,BE的中点分别为点P、Q,
∴AP=BQ,
∵△ACD≌△BCE,
∴∠CAP=∠CBQ,
在△ACP和△BCQ中,
,
∴△ACP≌△BCQ(SAS),
∴CP=CQ,且∠ACP=∠BCQ,
又∵∠ACP+∠PCB=90°,
∴∠BCQ+∠PCB=90°,
∴∠PCQ=90°,
∴△CPQ为等腰直角三角形.
∴∠ACD=∠BCE,
在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS),
∴BE=AD;
(2)如图1,∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∵△ABC中,∠BAC+∠ABC=180°-α,
∴∠BAM+∠ABM=180°-α,
∴△ABM中,∠AMB=180°-(180°-α)=α;
(3)△CPQ为等腰直角三角形.
证明:如图2,由(1)可得,BE=AD,
∵AD,BE的中点分别为点P、Q,
∴AP=BQ,
∵△ACD≌△BCE,
∴∠CAP=∠CBQ,
在△ACP和△BCQ中,
|
∴△ACP≌△BCQ(SAS),
∴CP=CQ,且∠ACP=∠BCQ,
又∵∠ACP+∠PCB=90°,
∴∠BCQ+∠PCB=90°,
∴∠PCQ=90°,
∴△CPQ为等腰直角三角形.
看了 如图①,CA=CB,CD=C...的网友还看了以下:
excel求出一列中的最大值和最小值,并以红色、绿色表示,并求出除最大和最小值以外数的平均值.在A 2020-05-16 …
在Excel中,求显示余数,32除以8余数为0,显示余数时也为0,要求显示为8如何做?在Excel 2020-05-17 …
初一科学题已知100毫升酒精的质量为80克,根据图乙所示示数,求混合后液体的密度?写出计算过程已知 2020-05-23 …
在图(a)所示的电路中,电源电压为15伏且保持不变,电阻R1的阻值为30欧.闭合电键S,电流表的示 2020-06-16 …
(2013•上海)在如图1所示的电路中,电源电压为18伏保持不变,电阻R1为10欧,闭合电键S后, 2020-06-16 …
如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示-根号2,设点B所表示的数为m.(1) 2020-06-27 …
如图2,一只蚂蚁从点A沿数轴向右直爬3个单位到达点B,点A表示-1,设点B所表示的数为m.(1)求 2020-06-27 …
求达人帮忙完成两道PLC设计题设计题1、请编写梯形图,使Y0输出周期为2秒,高低电平比为1:3的方 2020-06-29 …
设某厂家打算生产一批产品投放市场,已知该商品的需求函数为P(Q)=10e^-Q/2,且最大需求量为6 2020-12-31 …
如图所示电路图中,R为定值电阻,R'为电阻箱.先将开关S拨到触点1,调节电阻箱阻值R'=20Ω时,电 2020-12-31 …