早教吧作业答案频道 -->数学-->
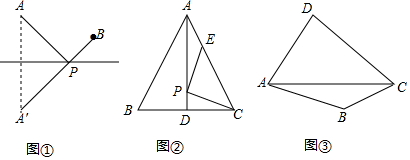
新知理解如图①,若点A、B在直线l同侧,在直线l上找一点P,使AP+BP的值最小.作法:作点A关于直线l的对称点A',连接A'B交直线l于点P,则点P即为所求.解决问题如图②,AD是边长为
题目详情
【新知理解】
如图①,若点A、B在直线l同侧,在直线l上找一点P,使AP+BP的值最小.
作法:作点A关于直线l的对称点A',连接A'B交直线l于点P,则点P即为所求.
【解决问题】
如图②,AD是边长为6cm的等边三角形ABC的中线,点P、E分别在AD、AC上,则PC+PE的最小值为___cm;
【拓展研究】
如图③,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.(保留作图痕迹,并对作图方法进行说明)
如图①,若点A、B在直线l同侧,在直线l上找一点P,使AP+BP的值最小.
作法:作点A关于直线l的对称点A',连接A'B交直线l于点P,则点P即为所求.
【解决问题】
如图②,AD是边长为6cm的等边三角形ABC的中线,点P、E分别在AD、AC上,则PC+PE的最小值为___cm;
【拓展研究】
如图③,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.(保留作图痕迹,并对作图方法进行说明)

▼优质解答
答案和解析
(1)【解决问题】
如图②,作点E关于AD的对称点F,连接PF,则PE=PF,
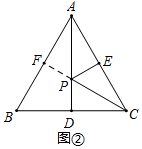
当点F,P,C在一条直线上时,PC+PE=PC+PF=CF(最短),
当CF⊥AB时,CF最短,此时BF=
AB=3(cm),
∴Rt△BCF中,CF=
=
=3
(cm),
∴PC+PE的最小值为3
cm,
故答案为:3
;
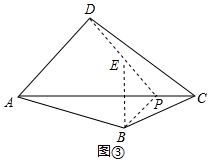
(2)【拓展研究】
方法1:如图③,作B关于AC的对称点E,连接DE并延长,交AC于P,点P即为所求,连接BP,则∠APB=∠APD.
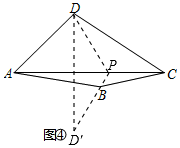
方法2:如图④,作点D关于AC的对称点D',连接D'B并延长与AC的交于点P,点P即为所求,连接DP,则∠APB=∠APD.
如图②,作点E关于AD的对称点F,连接PF,则PE=PF,

当点F,P,C在一条直线上时,PC+PE=PC+PF=CF(最短),
当CF⊥AB时,CF最短,此时BF=
| 1 |
| 2 |
∴Rt△BCF中,CF=
| BC2-BF2 |
| 62-32 |
| 3 |
∴PC+PE的最小值为3
| 3 |
故答案为:3
| 3 |
(2)【拓展研究】
方法1:如图③,作B关于AC的对称点E,连接DE并延长,交AC于P,点P即为所求,连接BP,则∠APB=∠APD.

方法2:如图④,作点D关于AC的对称点D',连接D'B并延长与AC的交于点P,点P即为所求,连接DP,则∠APB=∠APD.

看了 新知理解如图①,若点A、B在...的网友还看了以下:
如图8-5所示,竖直放置的U形管,左端开口右端封闭,管内有a、b两端水银柱,将A、B两段空气柱封闭 2020-04-07 …
直角三角形中,两条直角边a,b和斜边c之间满足下面的关系:a2+b2=c2.如果一个直角三角形的斜 2020-05-13 …
已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点F1,F2,M是椭圆上任意一点,若以坐 2020-05-14 …
已知椭C:x2a2+y2b2=1(a>b>0)的焦点为F1,F2,P是椭圆上任意一点,若以坐标原点 2020-05-14 …
已知椭圆C:x^2/a^2+y^2/b^2=1(a>b>0)的焦点为F1,F2,P是椭圆上任意一点 2020-05-14 …
人教版第四课时整式的乘法(1)如图是一个长方形娱乐场,其宽为a,长为2/3a,在这个娱乐场中有一个 2020-05-20 …
已知圆c经过P(4,-2)Q(-1,3)两点,且在y轴上截得的线段长为4根号3,半径小于5.若直线 2020-07-22 …
如图,以O为圆,AB长为直径作圆,在O上取一点,延长AB至点D,连接DC,过点A作O的切线交DC的 2020-07-31 …
一到画图题100分谁要?按下面步骤画图:1.任意做一条直线l,在l上任取一点a;2.过a点画直线l的 2020-10-31 …
已知x、y为正数,且|x^2-4|+(y^2-16)^2=0已知xy为正数,且|x^2-4|+(y^ 2020-11-20 …