如图，抛物线y=ax2+bx+c的对称轴是x=-1．且过点（12，0），有下列结论：①abc>0；②a-2b+4c=0；③25a-10b+4c=0；④3b+2c>0；⑤a-b≥m（am-b）；其中所有正确的结论是（）A.①②③B.①

Question

如图，抛物线y=ax²+bx+c的对称轴是x=-1．且过点（

(1)/(2)，0），有下列结论：①abc>0；  
②a-2b+4c=0； ③25a-10b+4c=0； ④3b+2c>0； ⑤a-b≥m（am-b）；
其中所有正确的结论是（　　）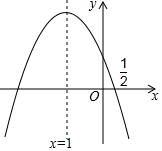

A. ①②③

B. ①③④

C. ①②③⑤

D. ①③⑤

Answer 1

由抛物线的开口向下可得：a<0，
根据抛物线的对称轴在y轴左边可得：a，b同号，所以b<0，
根据抛物线与y轴的交点在正半轴可得：c>0，
∴abc>0，故①正确；
直线x=-1是抛物线y=ax²+bx+c（a≠0）的对称轴，所以-(b)/(2a)=-1，可得b=2a，
a-2b+4c=a-4a+4c=-3a+4c，
∵a<0，
∴-3a>0，
∴-3a+4c>0，
即a-2b+4c>0，故②错误；
∵抛物线y=ax²+bx+c的对称轴是x=-1．且过点（(1)/(2)，0），
∴抛物线与x轴的另一个交点坐标为（-(5)/(2)，0），
当x=-(5)/(2)时，y=0，即a（-(5)/(2)）²+b×（-(5)/(2)）+c=0，
整理得：25a-10b+4c=0，故③正确；
∵b=2a，a+b+c<0，
∴(1)/(2)b+b+c<0，
即3b+2c<0，故④错误；
∵x=-1时，函数值最大，
∴a-b+c>m²a-mb+c（m≠-1），
∴a-b>m（am-b），所以⑤正确；
故选D．