如图，四边形ABCD，AD与BC不平行，AB=CD．AC，BD为四边形ABCD的对角线．E，F，G，H分别是BD，BC，AC，AD的中点．下列结论：①EG⊥FH；②四边形EFGH是矩形；③HF平分∠EHG；④EG=12（BC-AD）；⑤四边

Question

如图，四边形ABCD，AD与BC不平行，AB=CD．AC，BD为四边形ABCD的对角线．E，F，G，H分别是BD，BC，AC，AD的中点．
下列结论：①EG⊥FH；
②四边形EFGH是矩形；
③HF平分∠EHG；
④EG=

(1)/(2)（BC-AD）；
⑤四边形EFGH是菱形．
其中正确的个数是（　　）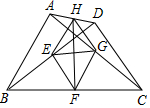

A. 1个

B. 2个

C. 3个

D. 4个

Answer 1

∵E，F分别是BD，BC的中点，
∴EF是△BCD的中位线，
∴EF=(1)/(2)CD，
同理可得，GH=(1)/(2)CD，FG=(1)/(2)AB，EH=(1)/(2)AB，
又∵AB=CD，
∴EF=FG=GH=HE，
∴四边形EFGH是菱形，故⑤正确，②错误，
∴EG⊥FH，HF平分∠EHG，故①、③正确，
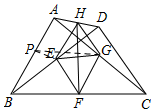
如图所示，取AB的中点P，连接PE，PG，
∵E是BD的中点，G是AC的中点，
∴PE是△ABD的中位线，PG是△ABC的中位线，
∴PE=(1)/(2)AD，PG=(1)/(2)BC，PE∥AD，PG∥BC，
∵AD与BC不平行，
∴PE与PG不平行，
∴△PEG中，EG>PG-PE，
∴EG>(1)/(2)BC-(1)/(2)AD，即EG>(1)/(2)（BC-AD），故④错误．
综上所述，正确的有①③⑤．
故选：C．