早教吧作业答案频道 -->数学-->
某校2017届高三文(1)班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生数有14人.(1)求总人数N和分数在120~125的人数n;(2)利用频率分布
题目详情
某校2017届高三文(1)班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生数有14人.
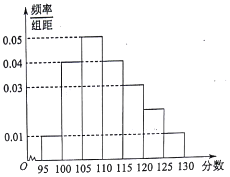
(1)求总人数N和分数在120~125的人数n;
(2)利用频率分布直方图,估算该班学生数学成绩的众数和中位数各是多少?
(3)现猪呢比从分数在115~120名学生(男女生比例为1:2)中任选2人,求其中至多含有1名男生的概率.

(1)求总人数N和分数在120~125的人数n;
(2)利用频率分布直方图,估算该班学生数学成绩的众数和中位数各是多少?
(3)现猪呢比从分数在115~120名学生(男女生比例为1:2)中任选2人,求其中至多含有1名男生的概率.
▼优质解答
答案和解析
(1)分数在110-120内的学生的频率为P1=(0.04+0.03)×5=0.35,
所以该班总人数为N=
=40.
分数在120-125内的学生的频率为:P2=1-(0.01+0.04+0.05+0.04+0.03+0.01)×5=0.10,
分数在120-125内的人数为n=40×0.10=4.
(2)由频率直方图可知众数是最高的小矩形底边中点的横坐标,
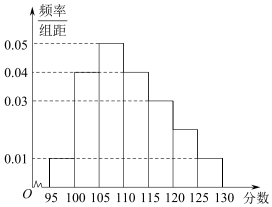
即为
=107.5.
设中位数为a,∵0.01×5+0.04×5+0.05×5+0.50,∴a=110.
∴众数和中位数分别是107.5,110.
(3)由题意分数在115-120内有学生40×(0.03×5)=6名,其中男生有2名.
设女生为A1,A2,A3,A4,男生为B1,B2,从6名学生中选出2名的基本事件为:
(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),
(A2,B1),(A2,B2),(A3,A4),(A3,B1),(A3,B2),(A3,B1),(A4,B1),
(A3,B1),(A4,B2),(A3,B1),(B1,B2),共15种,
其中至多有1名男生的基本事件共14种,
∴其中至多含有1名男生的概率为P=
.
所以该班总人数为N=
| 14 |
| 0.35 |
分数在120-125内的学生的频率为:P2=1-(0.01+0.04+0.05+0.04+0.03+0.01)×5=0.10,
分数在120-125内的人数为n=40×0.10=4.
(2)由频率直方图可知众数是最高的小矩形底边中点的横坐标,

即为
| 105+110 |
| 2 |
设中位数为a,∵0.01×5+0.04×5+0.05×5+0.50,∴a=110.
∴众数和中位数分别是107.5,110.
(3)由题意分数在115-120内有学生40×(0.03×5)=6名,其中男生有2名.
设女生为A1,A2,A3,A4,男生为B1,B2,从6名学生中选出2名的基本事件为:
(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),
(A2,B1),(A2,B2),(A3,A4),(A3,B1),(A3,B2),(A3,B1),(A4,B1),
(A3,B1),(A4,B2),(A3,B1),(B1,B2),共15种,
其中至多有1名男生的基本事件共14种,
∴其中至多含有1名男生的概率为P=
| 14 |
| 15 |
看了 某校2017届高三文(1)班...的网友还看了以下:
三峡旅行社推出“瀑布风景区一日游”的两种出游价格方案.①成人8人,儿童2人,选哪个方案买票比较合算 2020-04-13 …
古诗1.举杯邀明月,对影成?人.2.酒债寻常行处有,人生?古来稀.3.南朝?寺,多少楼台烟雨中. 2020-05-20 …
3成人2小孩乘船游玩,1号船最多乘3人,2号船最多乘2人,3号船只能乘1人,他们任选2只船或三只船 2020-06-16 …
一般情况下成人腋下正常的体温是℃,如图所示,小孩发烧时,常用凉湿毛巾敷在额头上通过水分的(填物态变 2020-07-05 …
帮帮忙做下成人英语卷子A.阅读下列短文,从A、B、C三个选项中最佳选项填在括号内.1.Dearal 2020-07-15 …
字谜:1.倒下一人2.尘土飞扬3.扑灭火星4.早有苗头 2020-07-23 …
有6本不同的书,按下列条件,各有多少种不同的分法?1:分成三堆,每堆两本2:分给甲乙丙三人,每人2本 2020-11-10 …
某校六年级原有2个班.现在重新编为3个班,将原1班人数的1/2与原2班的1/5组成新1班,将原来1班 2020-11-10 …
100人站成一排,从左到右进行“1、2”报数,报“1”的走开,剩下的人继续进行“1、2”报数.如此下 2020-11-17 …
四(1)班本次数学测试第一小组同学成绩如下表:成绩100分97分95分94分91分89分74分人数1 2020-11-18 …