早教吧作业答案频道 -->数学-->
某中学随机抽取50名高一学生调查其每天运动的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,运动的时间的范围是[0,100],样本数据分组为[0,20),[20,40)
题目详情
某中学随机抽取50名高一学生调查其每天运动的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,运动
的时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
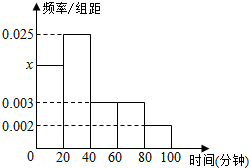
(1)求直方图中x的值;
(2)定义运动的时间不少于1小时的学生称为“热爱运动”,若该校有高一学生1200人,请估计有多少学生“热爱运动”;
(3)设m,n表示在抽取的50人中某两位同学每大运动的时间,且已知m,n∈[40,60)∪[80,100],求事件“|m-n|>20”的概率.
的时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].

(1)求直方图中x的值;
(2)定义运动的时间不少于1小时的学生称为“热爱运动”,若该校有高一学生1200人,请估计有多少学生“热爱运动”;
(3)设m,n表示在抽取的50人中某两位同学每大运动的时间,且已知m,n∈[40,60)∪[80,100],求事件“|m-n|>20”的概率.
▼优质解答
答案和解析
(1)由频率分布直方图,得:20×(0.002+0.003×2+x+0.025)=1,
解得x=0.017.
(2)由频率分布图得运动时间不少于1小时的频率为:
20×(0.002+0.003)=0.1,
∴估计有1200×0.1=120名学生“热爱运动”;
(3)由直方图得成绩在[40,60)的人数为50×20×0.003=3人,设为A、B、C,
成绩在[80,100]的人数为50×20×0.002=2人,设为x,y,
若m,n∈[40,60),[80,100]内时,则有Ax,Ay,Bx,By,Cx,Cy,共有6种情况,
所以基本事件总数为10种,
事件“|m-n|>20”所包含的基本事件个数有6种,
∴P(|m-n|>20)=
=
.
解得x=0.017.
(2)由频率分布图得运动时间不少于1小时的频率为:
20×(0.002+0.003)=0.1,
∴估计有1200×0.1=120名学生“热爱运动”;
(3)由直方图得成绩在[40,60)的人数为50×20×0.003=3人,设为A、B、C,
成绩在[80,100]的人数为50×20×0.002=2人,设为x,y,
若m,n∈[40,60),[80,100]内时,则有Ax,Ay,Bx,By,Cx,Cy,共有6种情况,
所以基本事件总数为10种,
事件“|m-n|>20”所包含的基本事件个数有6种,
∴P(|m-n|>20)=
| 6 |
| 10 |
| 3 |
| 5 |
看了 某中学随机抽取50名高一学生...的网友还看了以下:
高数改错题指出以下过程的错误之处.已知二元函数f(x,y)在x轴和y轴上函数值为1,其它所有点函数 2020-05-13 …
下列正确的是A单位质量的某种物质温度升高1℃所吸收的热量叫比热容B比热容与热量有关某种物质吸收或放 2020-05-15 …
物理难题,高手进某人用动滑轮组将重为700N的物体匀速提升0.2m高,所用拉力为250N,且移植在 2020-06-10 …
某桥桥下为通航河流,河道设计水位863m,设计最高通航水位860.50m,桥梁为T型,结构高度1. 2020-07-16 …
数学题(分式方程).某人用100元钱从市场上购买了某种杂志,按该杂志的定价3元出售,并很快售完.由 2020-08-02 …
如图所示,此时ABC弧线上的太阳高度角为0°,某学生正距B地正南方2775km的某地观测到北极星的仰 2021-01-17 …
如图所示,此时ABC弧线上的太阳高度角为0°,某学生在距离B地正南方2775千米的某地用肉眼观测到北 2021-01-17 …
如下图所示。此时ABC弧线上的太阳高度角为0°,某人正在距离B地正南方2775km的某地肉眼观测北极 2021-01-17 …
如下图所示,此时ABC弧线上的太阳高度角为0°,某人正在距离B地正南方2775km的某地肉眼观测北极 2021-01-17 …
如下图所示,此时ABC弧线上的太阳高度角为0°,某人正在距离B地正南方2775km的某地肉眼观测北极 2021-01-17 …