早教吧作业答案频道 -->数学-->
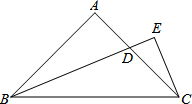
等腰直角三角形ABC中,∠A=90°,∠B的平分线交AC于D,过点C向BD做垂线,并与BD延长线交于点E,求证:BD=2CE.
题目详情
等腰直角三角形ABC中,∠A=90°,∠B的平分线交AC于D,过点C向BD做垂线,并与BD延长线交于点E,求证:BD=2CE.

▼优质解答
答案和解析
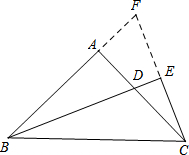 证明:延长CE,交BA延长线于点F.
证明:延长CE,交BA延长线于点F.
∵BE平分∠ABC,
∴∠ABD=∠DBC,
又∵BE⊥EC,
∴∠BEC=∠BEF=90°,
在△BEF和△BEC中,
,
∴△BEF≌△BEC,
∴EF=EC,
即CF=2EC,
∵AB=AC,∠BAC=90°
∴∠CAF=90°
Rt△ABD中,∠ABD+∠ADB=90°,
Rt△AEF中,∠ABD+∠F=90°,
∴∠ADB=∠F,
在△ABD和△ACF中,
,
∴△ABD≌△ACF,
∴BD=CF,
∵CF=2EC,
∴BD=2CE.
 证明:延长CE,交BA延长线于点F.
证明:延长CE,交BA延长线于点F.∵BE平分∠ABC,
∴∠ABD=∠DBC,
又∵BE⊥EC,
∴∠BEC=∠BEF=90°,
在△BEF和△BEC中,
|
∴△BEF≌△BEC,
∴EF=EC,
即CF=2EC,
∵AB=AC,∠BAC=90°
∴∠CAF=90°
Rt△ABD中,∠ABD+∠ADB=90°,
Rt△AEF中,∠ABD+∠F=90°,
∴∠ADB=∠F,
在△ABD和△ACF中,
|
∴△ABD≌△ACF,
∴BD=CF,
∵CF=2EC,
∴BD=2CE.
看了 等腰直角三角形ABC中,∠A...的网友还看了以下:
平行四边形的几何体.在平行四边形abcd,对角线BD、AC交于点O,BE为∠DBA的平分线,交AC 2020-06-06 …
物理:关于并联分流作用串联一个电阻可以分压,即串联一个定植电阻,可以分的一部分电压,但是并联可以分 2020-06-07 …
如图,在三角形ABC中,BD是角ABC的平分线,BC=6,AC=8,AB=10(1)画图,画出点c 2020-06-27 …
关于正态分布的分布密度曲线的途述:(1)曲线关于直线x=μ对称并且曲线在x轴上方;(2)曲线关于y 2020-07-04 …
菱形的两条对角线分别等于8和6,并且分别放置在X轴Y轴上,对角线的交点和原点重合.求各边所在的直线 2020-07-12 …
关于前线分子轨道的问题我能用它解释H2与N2的反应以及N2与O2的反应为什么需要催化剂,但H2与O2 2020-11-20 …
1.炫光是什么?不要百科里的,看不懂.2.关于并联分流的问题:并联电路各支路的电压是一样的,电阻又是 2020-11-21 …
关于雪线分布的说法,正确的是()A.乞力马扎罗山的南坡雪线高于北坡B.喜马拉雅山的南坡雪线高于北坡C 2020-12-05 …
多个电阻串联,并联多个电阻串联,相当于多根导线串联起来,由于导线的总长度比一个电阻的长度更长,所以总 2020-12-26 …
欧姆定律多个电阻串联,相当于多根导线串联起来,由于导线的总长度比一个电阻的长度更长,所以总电阻一定比 2020-12-26 …