早教吧作业答案频道 -->数学-->
直线c、d分别被直线a、b所截，且∠3+∠4=180°，求证：∠2+∠5=180°．证明：∵∠3+∠4=180°（已知）∴c∥d（）∴（两直线平行，同旁内角互补）∵∠1=（）∴∠2+∠5=180°．
题目详情
直线c、d分别被直线a、b所截，且∠3+∠4=180°，求证：∠2+∠5=180°．
证明：∵∠3+∠4=180°（已知）
∴c∥d （___）
∴___（两直线平行，同旁内角互补）
∵∠1=___（___）
∴∠2+∠5=180°___．
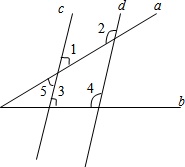
证明：∵∠3+∠4=180°（已知）
∴c∥d （___）
∴___（两直线平行，同旁内角互补）
∵∠1=___（___）
∴∠2+∠5=180°___．
▼优质解答
答案和解析
证明：∵∠3+∠4=180°（已知）
∴c∥d （同旁内角互补，两直线平行 ）
∴∠1+∠2=180°（两直线平行，同旁内角互补）
∵∠1=∠5（ 对顶角相等）
∴∠2+∠5=180°（等量代换）．
故答案为：同旁内角互补，两直线平行；∠1+∠2=180°；∠5；对顶角相等；等量代换．
∴c∥d （同旁内角互补，两直线平行 ）
∴∠1+∠2=180°（两直线平行，同旁内角互补）
∵∠1=∠5（ 对顶角相等）
∴∠2+∠5=180°（等量代换）．
故答案为：同旁内角互补，两直线平行；∠1+∠2=180°；∠5；对顶角相等；等量代换．
看了 直线c、d分别被直线a、b所...的网友还看了以下：
直线的倾斜角是指与X轴的夹角还是指与Y轴的夹角?已知直线的斜率是1那直线的倾斜角是45还是135? 2020-06-06 …
已知A={三角形}B={等腰三角形}C={等边三角形}D={直角三角形}用维恩图表示他们之间的关系 2020-07-12 …
已知a，b，c是△ABC的三条边长，且关于x的方程（c-b）x2+2（b-a）x+（a-b）=0有 2020-07-21 …
已知直角三角形两直角边长度,求底边夹角已知直角三角形两直边长度200,3750,求三角形其他两个内 2020-07-22 …
如图，D是等边△ABC的边AB上的一点，CD=BE，∠1=∠2，则△ADE是（）A.等腰三角形B. 2020-07-29 …
这道题是不是有误呢?若无误,又应选哪个?设A={x\x是直角三角形},B={x\x是等腰三角形}, 2020-07-30 …
在极坐标系下，已知点A(−2，−π2)，B(2，3π4)，O(0，0)，则△ABO为（）A.正三角 2020-08-02 …
在三角形ABC中,已知角A等于60度,BD垂直AC,CE垂直AB,且BD等于CF则三角形ABC是什 2020-08-03 …
数学题在线解答已知集合A={三角形},B={等腰三角形},C={等边三角形},D={直角三角形},那 2020-11-27 …
有关利用三角函数知识,求直线的斜率倾斜角已知直线AB的斜率为4/3,直线L的倾斜角是直线AB倾斜角的 2020-12-08 …