现有3个命题：P1：函数f（x）=lgx-|x-2|有2个零点．P2：面值为3分和5分的邮票可支付任何n（n>7，n∈N）分的邮资．P3：若a+b=c+d=2，ac+bd>4，则a、b、c、d中至少有1个为负数．那么，这3个命题

Question

现有3个命题：
P₁：函数f（x）=lgx-|x-2|有2个零点．
P₂：面值为3分和5分的邮票可支付任何n（n>7，n∈N）分的邮资．
P₃：若a+b=c+d=2，ac+bd>4，则a、b、c、d中至少有1个为负数．
那么，这3个命题中，真命题的个数是（　　）

A. 0

B. 1

C. 2

D. 3

Answer 1

令f（x）=lgx-|x-2|=0，得到lgx=|x-2|，
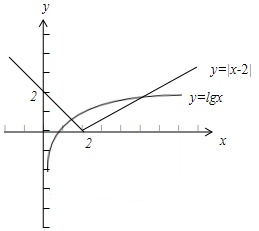
作出y=lgx，y=|x-2|的图象可知，它们有2个交点，
从而函数f（x）=lgx-|x-2|有2个零点，故p₁是真命题；
P₂：面值为3分和5分的邮票可支付任何n（n>7，n∈N）分的邮资，是真命题．
用数学归纳法证明：
①当n=8，9，10时，由8=3+5，9=3+3+3，10=5+5，知命题成立；
②假设当n=k（k>7，n∈N）时，命题成立，则k=8+3m，或k=9+3m，或k=10+3m，m∈N^*，
∴当n=k+1时，则n=9+3m，或n=10+3m，或n=11+3m=8+3（m+1），m∈N^*，
∴当n=k+1时，命题成立．
由①②知P₂：面值为3分和5分的邮票可支付任何n（n>7，n∈N）分的邮资，是真命题．
P₃：若a+b=c+d=2，ac+bd>4，则a、b、c、d中至少有1个为负数，是真命题．
用反证法证明：
假设a，b，c，d没有1 个为负数，即a≥0，b≥0，c≥0，d≥0，∴ad+bc≥0，
∵a+b=c+d=2，∴（a+b）（c+d）=ac+bd+ad+bc=4，
∵ac+bd>4，∴ad+bc<0，
这与ad+bc≥0矛盾，故假设不成立，
∴若a+b=c+d=2，ac+bd>4，则a、b、c、d中至少有1个为负数，
故P₃为真命题．
故选：D．