早教吧作业答案频道 -->数学-->
探究与发现:如图①,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.(1)当∠BAD=60°时,求∠CDE的度数;(2)当点D在BC(点B、C除外)上运动时,试猜想并探究∠BAD与∠CDE
题目详情
探究与发现:如图①,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.
(1)当∠BAD=60°时,求∠CDE的度数;
(2)当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系;
(3)深入探究:若∠BAC≠90°,试就图②探究∠BAD与∠CDE的数量关系.
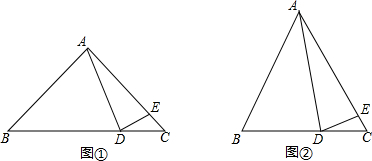
(1)当∠BAD=60°时,求∠CDE的度数;
(2)当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系;
(3)深入探究:若∠BAC≠90°,试就图②探究∠BAD与∠CDE的数量关系.

▼优质解答
答案和解析
(1)∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,
∵∠BAD=60°,
∴∠DAE=30°,
∵AD=AE,
∴∠AED=75°,
∴∠CDE=∠AED=∠C=30°;
(2)设∠BAD=x,
∴∠CAD=90°-x,
∵AE=AD,
∴∠AED=45°+
x,
∴∠CDE=
x;
(3)设∠BAD=x,∠C=y,
∵AB=AC,∠C=y,
∴∠BAC=180°-2y,
∵∠BAD=x,
∴∠DAE=y+
x,
∴∠CDE=∠AED-∠C=
x.
∴∠B=∠C=45°,
∵∠BAD=60°,
∴∠DAE=30°,
∵AD=AE,
∴∠AED=75°,
∴∠CDE=∠AED=∠C=30°;
(2)设∠BAD=x,
∴∠CAD=90°-x,
∵AE=AD,
∴∠AED=45°+
| 1 |
| 2 |
∴∠CDE=
| 1 |
| 2 |
(3)设∠BAD=x,∠C=y,
∵AB=AC,∠C=y,
∴∠BAC=180°-2y,
∵∠BAD=x,
∴∠DAE=y+
| 1 |
| 2 |
∴∠CDE=∠AED-∠C=
| 1 |
| 2 |
看了 探究与发现:如图①,在Rt△...的网友还看了以下:
关于一个双曲线的难题,在线等待!急啊!大家帮帮忙吧!设AB是双曲线x^2-y^2除以2=1,上的2 2020-05-15 …
正方体ABCD-A'B'C'D'的棱长为8,M.N.P分别是A'B',AD,BB'的中点.(1)画 2020-05-16 …
1.如图所示,在三角形ABC中,角BCA=90度,延长B到点D,使AD=1/2AB,点E,F分别为 2020-05-17 …
如图已知△abc中,ab=ac=18cm,点d位ab的中点(1)如果点P在线段BC上以3厘米每秒的 2020-06-07 …
已知圆C:x^2+y^2+ax-4y+1=0(a属于R),过定点P(0,1)作斜率为1的直线交圆C 2020-06-09 …
某数学兴趣小组在探求线段中点坐标时经历了如下过程特别探究在图甲中,已知点E、F分别为线段AB、CD 2020-06-11 …
如图已知点abcde在同一直线上,且AC等于BD,E是线段BC的中点.(1)点e是如图已知点abc 2020-06-15 …
已知双曲线x^2-y^2/2=1与点P(1,2),过P点作直线l与双曲线交于A、B两点,若P为AB 2020-06-16 …
正方体ABCD-A1B1C1D1,棱长为1、,点F是A1D中点.1.证明:A1B平行面AFC2.求 2020-06-21 …
已知双曲线X^2-Y^2/2=1与点P(1,2),过点P作直线L交双曲线于A、B两点,诺P为AB的 2020-06-29 …