早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,A(a,0),B(0,b),其中b>a>0,点C在第一象限,BA⊥BC,BA=BC,点F在线段OB上,OA=OF,AF的延长线与CB的延长线交于点D,AB与CF交于点E.(1)直接写出点C的
题目详情
如图,在平面直角坐标系中,A(a,0),B(0,b),其中b>a>0,点C在第一象限,BA⊥BC,BA=BC,点F在线段OB上,OA=OF,AF的延长线与CB的延长线交于点D,AB与CF交于点E.
(1)直接写出点C的坐标:___(用含a,b的式子表示);
(2)求证:∠BAF=∠BCE;
(3)设点C关于直线AB的对称点为M,点C关于直线AF的对称点为N.求证:M,N关于x轴对称.

(1)直接写出点C的坐标:___(用含a,b的式子表示);
(2)求证:∠BAF=∠BCE;
(3)设点C关于直线AB的对称点为M,点C关于直线AF的对称点为N.求证:M,N关于x轴对称.

▼优质解答
答案和解析
 (1) 如图1,过C点作CP⊥y轴于点P,
(1) 如图1,过C点作CP⊥y轴于点P,
∵CP⊥y轴,
∴∠BPC=90°,
∴∠BPC=∠AOB,
∵AB⊥BC,
∴∠ABC=90°,
∴∠ABO+∠CBP=90°,
∵∠ABO+∠BAO=90°,
∴∠CBP=∠BAO,
在△AOB与△BEC中,
,
∴△AOB≌△BPC(AAS),
∴CE=OB=b,BE=OA=a,
∴OP=OB+BP=a+b,
∴点C的坐标为(b,a+b),
故答案为:(b,a+b);
(2)证明:∵△AOB≌△BPC,
∴BP=OA=OF,CP=BO,
∴FP=OB=CP,
∴∠PFC=45°,∠AFC=90°,
∴∠BAF=∠BCE;
(3)证明:如图2,∵点C关于直线AB的对称点为M,点C关于直线AF的对称点为N,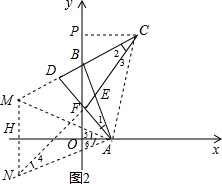
∴AM=AC,AN=AC,
∴AM=AN,
∵∠1=∠5,∠1=∠6,
∴∠5=∠6,
在△MAH与△NAH中,
∴
,
∴△MAH≌△NAH(SAS),
∴MH=NH,
∴M,N关于x轴对称.
 (1) 如图1,过C点作CP⊥y轴于点P,
(1) 如图1,过C点作CP⊥y轴于点P,∵CP⊥y轴,
∴∠BPC=90°,
∴∠BPC=∠AOB,
∵AB⊥BC,
∴∠ABC=90°,
∴∠ABO+∠CBP=90°,
∵∠ABO+∠BAO=90°,
∴∠CBP=∠BAO,
在△AOB与△BEC中,
|
∴△AOB≌△BPC(AAS),
∴CE=OB=b,BE=OA=a,
∴OP=OB+BP=a+b,
∴点C的坐标为(b,a+b),
故答案为:(b,a+b);
(2)证明:∵△AOB≌△BPC,
∴BP=OA=OF,CP=BO,
∴FP=OB=CP,
∴∠PFC=45°,∠AFC=90°,
∴∠BAF=∠BCE;
(3)证明:如图2,∵点C关于直线AB的对称点为M,点C关于直线AF的对称点为N,

∴AM=AC,AN=AC,
∴AM=AN,
∵∠1=∠5,∠1=∠6,
∴∠5=∠6,
在△MAH与△NAH中,
∴
|
∴△MAH≌△NAH(SAS),
∴MH=NH,
∴M,N关于x轴对称.
看了 如图,在平面直角坐标系中,A...的网友还看了以下:
如图所示,由于有风,河岸上的旗帜向右飘,在河面上A、B两艘船上的旗帜分别向右和向左飘,则这两艘的运 2020-04-06 …
在三角形ABC和三角形A'B'C'中,AB=A'B',BC=B'C',下面四个条件中,1)AC=A 2020-05-13 …
在三角形ABC中,角A,角B,角C=2:1:1,a,b,c分别是角A,角B,角C的对边 下列等式成 2020-05-15 …
如图.矩形纸片OABC放在平面直角坐标系内 OA,OC分别与X轴 Y轴重合 OA=8 OC=4 将 2020-05-16 …
利用有理数abc在数轴上的位置,化简a+|a+b|-|c|-|c-b|,将a,b,c,0,-a,- 2020-05-22 …
求证在三角形ABC和A'B'C'中,角A=角A',角B=B',AC+BC=A'C'+B'C',那么 2020-05-23 …
正余弦综合应用1.在三角形ABC中,a,b,c分别为三个内角A,B,C所对的边,两个向量P=(a+ 2020-06-03 …
如图表示长期使用一种农药后,害虫种群密度的变化情况.下列有关叙述不正确的是()A.A点种群中存在很 2020-06-06 …
证明:锐角三角形a²+b²>c²钝角三角形:a²+b²<c²证明:锐角三角形a²+b²>c²钝角三 2020-06-12 …
1.一个三角形中,内角小于90度的角至少有A.1个B.2个C.3个D.0个2.满足条件∠A=∠B= 2020-06-12 …