如图，AD、BE是△ABC的两条高，过点D作DF⊥AB，垂足为F，FD交BE于M，FD、AC的延长线交于点N．（1）求证：△BFM∽△NFA；（2）试探究线段FM、DF、FN之间的数量关系，并证明你的结论；（3）若AC=B

Question

如图，AD、BE是△ABC的两条高，过点D作DF⊥AB，垂足为F，FD交BE于M，FD、AC的延长线交于点N．

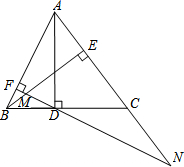
（1）求证：△BFM∽△NFA；
（2）试探究线段FM、DF、FN之间的数量关系，并证明你的结论；
（3）若AC=BC，DN=12，tanN=(1)/(2)，求线段AC的长．

Answer 1

（1）证明：∵DF⊥AB，AD、BE是△ABC的高，
∴∠BFD=∠AFD=∠AEB=∠ADB=90°，
∴∠FBM=90°-∠BAC，∠N=90°-∠BAC，
∴∠FBM=∠N，
∵∠FBM=∠N，∠BFD=∠AFD，
∴△BFM∽△NFA；
（2） DF²=FM•FN，理由为：
证明：∵△BFM∽△NFA，
∴(FB)/(FN)=(FM)/(FA)，
∴FM•FN=FB•FA，
∵∠FBD+∠FDB=90°，∠FBD+∠FAD=90°，
∴∠FDB=∠FAD，
∵∠BFD=∠AFD，∠FDB=∠FAD，
∴△BFD∽△DFA，
∴(FB)/(DF)=(DF)/(FA)，即DF²=FB•FA，
∴DF²=FM•FN；
（3） ∵AC=BC，
∴∠BAC=∠ABC，
∵∠ABC+∠FDB=∠BAC+∠N=90°，
∴∠FDB=∠N=∠FBM，
∴(FM)/(FB)=tan∠FBM=tanN=(1)/(2)，(FB)/(FD)=tan∠FDB=tanN=(1)/(2)，
∴FB=2FM，FD=2FB=4FM，
∵DF²=FM•FN，
∴（4FM）²=FM•（4FM+12），
解得：FM=1或FM=0（舍去），
∴FB=2，FD=4，FN=FD+DN=16，
∵(AF)/(FN)=tanN=(1)/(2)，
∴AF=8，AB=AF+BF=10，
在Rt△BFD中，BD=√(BF2+DF2)=√(22+42)=2√(5)，
在Rt△ADB和Rt△ADC中，AD²=AB²-BD²=AC²-CD²，
∴AC²-（AC-2√(5)）²=10²-（2√(5)）²，
解得：AC=5√(5)．