早教吧作业答案频道 -->数学-->
如图,正方体的棱长a,点C,D分别是两条棱的中点.(1)证明:四边形ABCD是一个梯形;(2)求四边形ABCD的面积.
题目详情
如图,正方体的棱长a,点C,D分别是两条棱的中点.
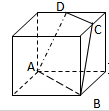
(1)证明:四边形ABCD是一个梯形;
(2)求四边形ABCD的面积.

(1)证明:四边形ABCD是一个梯形;
(2)求四边形ABCD的面积.
▼优质解答
答案和解析
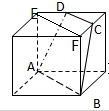
(1)连接EF,根据正方体的性质得出:
∵点C,D分别是两条棱的中点.
∴CD∥EF,EF∥AB,DC=
EF,
∴CD∥AB,CD=
AB,
∴四边形ABCD是一个梯形;
(2)∵正方体的棱长a,
∴AB=
a,CD=
,
h=
a=
a
∴四边形ABCD的面积=
×(
a+
)×
=
,
∵点C,D分别是两条棱的中点.
∴CD∥EF,EF∥AB,DC=
| 1 |
| 2 |
∴CD∥AB,CD=
| 1 |
| 2 |
∴四边形ABCD是一个梯形;

(2)∵正方体的棱长a,
∴AB=
| 2 |
| ||
| 2 |
h=
12+(
|
3
| ||
| 4 |
∴四边形ABCD的面积=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
| 9a2 |
| 8 |
看了 如图,正方体的棱长a,点C,...的网友还看了以下:
正方体ABCD-A’B"C"D"中P,Q,R分别是AB,AD,BC的中点,那么正方体的过P,Q,R 2020-05-13 …
四边形ABCD内有一点P到四条边AB.B四边形ABCD内有一点P到四条边AB.BC.CD.DA的距 2020-05-23 …
下列说法中错误的是()A.多边形是平面图形,平面图形不一定是多边形.B.四边形由四条线短组成,但四 2020-06-07 …
下列图形中能够密铺的有()a正方形;b四边形;c三角形;d正六边形;e正七边形;f正八边形.A.1 2020-06-23 …
四边形的周长为a,两条对角线的和为b,四边形的周长为a,两条对角线的和为b,成立的式子为:———— 2020-07-20 …
若一个多边形的每个外角都等于60°,则这个多边形是()A.三角形B.四边形C.五边形D.六边形 2020-07-29 …
若一个多边形的每个外角都等于60°,则这个多边形是()A.三角形B.四边形C.五边形D.六边形 2020-07-29 …
如图:已知点M、N、P、Q分别为菱形ABCD四边上的中点,下列说法正确的是()A.四边形MNPQ是 2020-07-30 …
用反证法证明真命题“四边形中至少有一个角是钝角或直角”时,应假设()A.四边形中至多有一个角是钝角 2020-08-01 …
如图,菱形ABCD中,对角线AC、BD相交于点O,M、N分别是边AB、AD的中点,连接OM、ON、M 2020-12-25 …