早教吧作业答案频道 -->数学-->
如图,四棱锥P-ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°.PA⊥面ABCD,且PA=3.F在棱PA上,且AF=1,E在棱PD上.(Ⅰ)若CE∥面BDF,求PE:ED的值;(Ⅱ)求二面角B-DF-A的大小.
题目详情
如图,四棱锥P-ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°.PA⊥面ABCD,且PA=3.F在棱PA上,且AF=1,E在棱PD上.
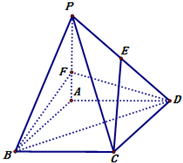
(Ⅰ)若CE∥面BDF,求PE:ED的值;
(Ⅱ)求二面角B-DF-A的大小.

(Ⅰ)若CE∥面BDF,求PE:ED的值;
(Ⅱ)求二面角B-DF-A的大小.
▼优质解答
答案和解析
证明:(Ⅰ)过E作EG∥FD交AP于G,连接CG,
连接AC交BD于O,连接FO.
∵EG∥FD,EG⊄面BDF,FD⊂面BDF,
∴EG∥面BDF,又EG∩CE=E,CE∥面BDF,EG,CE⊂面CGE,
∴面CGE∥面BDF,…(3分)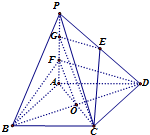
又CG⊂面CGE,∴CG∥面BDF,
又面BDF∩面PAC=FO,CG⊂面PAC,
∴FO∥CG.
又O为AC中点,∴F为AG中点,∴FG=GP=1,
∴E为PD中点,PE:ED=1:1.…(6分)
(Ⅱ)过点B作BH⊥直线DA交DA延长线于H,过点H作HI⊥直线DF交DF于I,…(8分)
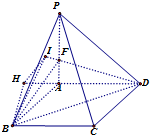
∵PA⊥面ABCD,∴面PAD⊥面ABCD,
∴BH⊥面PAD,由三垂线定理可得DI⊥IB,
∴∠BIH是二面角B-DF-A的平面角.
由题易得AH=
,BH=
,HD=
,
且
=
=
,∴HI=
,
∴tan∠BIH=
×
=
,…(10分)
∴二面角B-DF-A的大小为arcran
.…(12分)
连接AC交BD于O,连接FO.
∵EG∥FD,EG⊄面BDF,FD⊂面BDF,
∴EG∥面BDF,又EG∩CE=E,CE∥面BDF,EG,CE⊂面CGE,
∴面CGE∥面BDF,…(3分)

又CG⊂面CGE,∴CG∥面BDF,
又面BDF∩面PAC=FO,CG⊂面PAC,
∴FO∥CG.
又O为AC中点,∴F为AG中点,∴FG=GP=1,
∴E为PD中点,PE:ED=1:1.…(6分)
(Ⅱ)过点B作BH⊥直线DA交DA延长线于H,过点H作HI⊥直线DF交DF于I,…(8分)

∵PA⊥面ABCD,∴面PAD⊥面ABCD,
∴BH⊥面PAD,由三垂线定理可得DI⊥IB,
∴∠BIH是二面角B-DF-A的平面角.
由题易得AH=
| 3 |
| 2 |
3
| ||
| 2 |
| 9 |
| 2 |
且
| HI |
| HD |
| AF |
| DF |
| 1 | ||
|
9
| ||
| 20 |
∴tan∠BIH=
3
| ||
| 2 |
| 20 | ||
9
|
| ||
| 3 |
∴二面角B-DF-A的大小为arcran
| ||
| 3 |
看了 如图,四棱锥P-ABCD中,...的网友还看了以下:
设a=(√5-1)/2,求(a^5+a^4-2a^3-a^2-a+2)/a^3-a∵2a=√5-1 2020-04-05 …
读图,完成小题。小题1:美国的乳畜业主要分布在图中()A.A处B.B处C.C处D.D处小题2:乳畜 2020-04-07 …
⒈再△ABC核△A'B'C'中.∠A=∠A’,CD和C’D’分别是边AB和A’B’上的中线,再从以 2020-05-13 …
集合A={x|x=(a^2-2a+1)/(a-1),a属于整数,a不等于1},……集合A={x|x 2020-05-13 …
选出括号部分发音不同的单词1.(a)ppleswh(a)tw(a)nt2.(ru)bbersgl( 2020-06-20 …
设n阶矩阵A=E-a*a^T,其中a是n维非零列向量,证明1.A^2=A的充要条件是a^T*a设n 2020-06-23 …
C语言中二维数组a[i][j]中,a+i=*(a+i)=a[i]=&a[i]是怎么理解的.其中*( 2020-06-27 …
等腰直角△ABC中,∠ACB=90°,AC=BC,点D是斜边AB上一点,以CD为直角边作等腰直角△ 2020-06-27 …
如图为一个豌豆荚,内有6粒豌豆种子.图中a表示豌豆荚,b表示其中的一粒种子.下列有关叙述中,错误的 2020-06-28 …
(2014•苏州)如图为一个豌豆荚,内有6粒豌豆种子.图中a表示豌豆荚,b表示其中的一粒种子.下列 2020-06-28 …