设x1、x2是区间D上的任意两点，若函数y=f(x)满足f(成立则称函数y=f(x)在区间D上下凸.(1)证明函数f(x)=x+在区间(0+∞)上下凸.(2)若函数y=f(x)在区间D上下凸则对任意的x1x2…x

Question

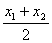设x ₁ 、x ₂ 是区间D上的任意两点，若函数y=f(x)满足f( 成立 则称函数y=f(x)在区间D上下凸.

(1)证明函数f(x)=x+ 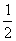在区间(0 +∞)上下凸.

(2)若函数y=f(x)在区间D上下凸 则对任意的x ₁ x ₂ … x _n ∈D 有 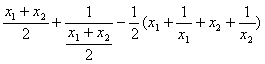.试根据下凸倒数的这一性质 证明若x ₁ x ₂ … x _n ∈(0 +∞) 则(x ₁ +x ₂ +…+x _n ) 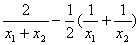≥n ² .

(文)已知S _n 是等比数列{a _n }的前n项和 且a ₃ a ₉ a ₆ 成等差数列 问:S ₃ S ₉ S ₆ 是否成等差数列?

Answer 1

答案：(理)证明:(1)设x1＞0 x2＞0 则f()-［f(x1)+f(x2)］= ===≤0 ∴f()≤［f(x1)+f(x2)］.由定义可知f(x)=x+在区间(0 +∞)上下凸. (2)由(1)可知f(x)=x+在(0 +∞)上下凸 根据性质 有∴. ∵x1 x2 … xn∈(0 +∞) ∴x1+x2+…+xn＞0.上述可化为(x1+x2+…+xn)≥n2. (文)由a3 a9 a6成等差数列，可得a3+a6=2a9 即a1q2+a1q5=2a1q8.∵a1q2≠0 ∴1+q3=2q6. 当q≠1时，S3+S6==2S9 ∴S3 S9 S6成等差数列. 当q=1时，S3+S6=3a1+6a1=9a1 而2S9=18a1.∵a1≠0 ∴S3+S6≠2S9.∴S3 S9 S6不成等差数列.综合 得当q≠1时，S3 S9 S6成等差数列，当q=1时，S3 S9 S6不成等差数列.