早教吧作业答案频道 -->数学-->
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点.(Ⅰ)证明:BC1∥平面A1CD;(Ⅱ)设AA1=AC=CB=2,AB=22,求四棱锥C-A1ABE的体积.
题目详情
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点.
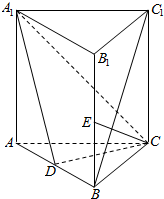
(Ⅰ)证明:BC1∥平面A1CD;
(Ⅱ)设AA1=AC=CB=2,AB=2
,求四棱锥C-A1ABE的体积.

(Ⅰ)证明:BC1∥平面A1CD;
(Ⅱ)设AA1=AC=CB=2,AB=2
| 2 |
▼优质解答
答案和解析
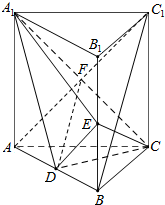 (Ⅰ)证明:连接AC1 交A1C于点F,则F为AC1的中点.
(Ⅰ)证明:连接AC1 交A1C于点F,则F为AC1的中点.
∵直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,故DF为三角形ABC1的中位线,故DF∥BC1.
由于DF⊂平面A1CD,而BC1不在平面A1CD中,故有BC1∥平面A1CD.
(Ⅱ) ∵AA1=AC=CB=2,AB=2
,
∴此直三棱柱的底面ABC为等腰直角三角形.
由D为AB的中点可得CD⊥平面ABB1A1 ,∴CD=
.
∴四棱锥C-A1ABE的体积V=
×
×CD=
×3
×
=2
 (Ⅰ)证明:连接AC1 交A1C于点F,则F为AC1的中点.
(Ⅰ)证明:连接AC1 交A1C于点F,则F为AC1的中点.∵直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,故DF为三角形ABC1的中位线,故DF∥BC1.
由于DF⊂平面A1CD,而BC1不在平面A1CD中,故有BC1∥平面A1CD.
(Ⅱ) ∵AA1=AC=CB=2,AB=2
| 2 |
∴此直三棱柱的底面ABC为等腰直角三角形.
由D为AB的中点可得CD⊥平面ABB1A1 ,∴CD=
| 2 |
∴四棱锥C-A1ABE的体积V=
| 1 |
| 3 |
| (AA1+BE)×AB |
| 2 |
| 1 |
| 3 |
| 2 |
| 2 |
看了 如图,直三棱柱ABC-A1B...的网友还看了以下:
已知a.b.c分别是三角形ABC的三个内角A.B.C所对的边,若三角形ABC面积S三角形ABC=2 2020-04-05 …
若b+c分之a=c+a分之b=a+b分之c,则a+b-3c分之2a+2b+c=或(2)若关于x的方 2020-04-06 …
A、B、C三人分别拿一只水桶到同一商店打水,他们打水所需的时间为3分钟、2分钟和4分钟.若按A-B 2020-04-11 …
分解因式:a²+2a(b+c)+(b+c)²=分解因式:(2x+y)²-(x+2y²)=(m+n) 2020-05-13 …
已知a+b+c=0,求a(b分之1+c分之1)+b(c分之1+a分之1)+c(a分之1+b分之1) 2020-05-15 …
设a.b.c分别是三角形ABC的三个内角A.B.C所对的边,由a2=b(b+c)知与满足的关系为 2020-05-15 …
1、已知:a+b+c=0,求:a(b分之1+c分之1)+b(c分之1+a分之1)+c(a分之1+b 2020-05-21 …
在△ABC中,a,b,c分别为角A,B,C所对的边,a,b,c成等差数列,且a=2c在△ABC中, 2020-06-04 …
若a加b加c等于0,化简a{b分之一加c分之一}加b{c分之一加a分之一}加c{a分之一加b分之一 2020-06-17 …
1.已知a.b.c为实数,且a+b分之aXb=三分之一,b+c分之bXc=四分之一,a+c分之aX 2020-06-27 …