早教吧作业答案频道 -->数学-->
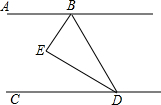
如图,已知AB∥CD,BE平分∠ABD,DE平分∠BDC,H是直线CD上一动点,(不与点D重合),BI平分∠HBD,写出∠EBI与∠HBD的数量关系,并说明理由.
题目详情
如图,已知AB∥CD,BE平分∠ABD,DE平分∠BDC,H是直线CD上一动点,(不与点D重合),BI平分∠HBD,写出∠EBI与∠HBD的数量关系,并说明理由.

▼优质解答
答案和解析
 ∠BHD=2∠EBI或∠BHD=180°-2∠EBI.
∠BHD=2∠EBI或∠BHD=180°-2∠EBI.
理由:∵BE平分∠ABD,
∴∠ABD=2∠EBD,
∵BI平分∠HBD,
∴∠HBD=2∠IBD,
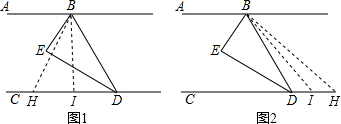
如图1,点H在点D的左边时,∠ABH=∠ABD-∠HBD,
∠EBI=∠EBD-∠IBD,
∴∠ABH=2∠EBI,
∵AB∥CD,
∴∠BHD=∠ABH,
∴∠BHD=2∠EBI;
如图2,点H在点D的右边时,∠ABH=∠ABD+∠HBD,
∠EBI=∠EBD+∠IBD,
∴∠ABH=2∠EBI,
∵AB∥CD,
∴∠BHD=180°-∠ABH,
∴∠BHD=180°-2∠EBI,
综上所述,∠BHD=2∠EBI或∠BHD=180°-2∠EBI.
 ∠BHD=2∠EBI或∠BHD=180°-2∠EBI.
∠BHD=2∠EBI或∠BHD=180°-2∠EBI.理由:∵BE平分∠ABD,
∴∠ABD=2∠EBD,
∵BI平分∠HBD,
∴∠HBD=2∠IBD,
如图1,点H在点D的左边时,∠ABH=∠ABD-∠HBD,
∠EBI=∠EBD-∠IBD,
∴∠ABH=2∠EBI,
∵AB∥CD,
∴∠BHD=∠ABH,
∴∠BHD=2∠EBI;
如图2,点H在点D的右边时,∠ABH=∠ABD+∠HBD,
∠EBI=∠EBD+∠IBD,
∴∠ABH=2∠EBI,
∵AB∥CD,
∴∠BHD=180°-∠ABH,
∴∠BHD=180°-2∠EBI,
综上所述,∠BHD=2∠EBI或∠BHD=180°-2∠EBI.
看了 如图,已知AB∥CD,BE平...的网友还看了以下:
提示:D-C=0A-B,A-D,D-C,D-E,E-F=1A-D,C-F=2A-B,D-E,E-F 2020-04-06 …
已知A,B为两种黑色粉末,D为红色金属物质,E为一种白色沉淀.A,B,C,D,E五种物质之间已知A 2020-05-17 …
已知A、B、C、D、E、F6种物质的转化关系如下:(1)A+B→C+H2O(2)C+KOH→D↓( 2020-06-05 …
下表是元素周期表的一部分,A、B、C、D、E、X是下表中给出元素组成的常见单质或化合物.已知A、B 2020-06-09 …
已知5个正数a,b,c,d,e的平均数为m,且a<b<c<d<e,则数据a,b,0,c,d,e的平均 2020-10-31 …
如图1,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD(BA≠BD);如图2,已知A 2020-11-01 …
已知△ABC的面积为1,D,E分别是AB,AC边上的点,CD,BE交于F点,过点F作FM‖AB,FN 2020-11-03 …
“我们可以得到A和B分别与C、D、E之间的关系”这句话用英语怎么表达“我们可以得到A和B分别与C、D 2020-12-25 …
七张卡片正面分别标有1,2,3,4,5,6,7七个数字,后面分别标有a,b,c,d,e,f、g七个字 2020-12-26 …
已知A、B、C、D、E五种物质之间存在以下的转化关系.其中A、C两种物质的组成元素相同,且常温下为液 2021-01-22 …