在平面直角坐标系xOy中，点A的坐标为（1，0），P是第一象限内任意一点，连接PO，PA，若∠POA=m°，∠PAO=n°，则我们把（m°，n°）叫做点P的“双角坐标”．例如，点（1，1）的“双

Question

在平面直角坐标系xOy中，点A的坐标为（1，0），P是第一象限内任意一点，连接PO，PA，若∠POA=m°，∠PAO=n°，则我们把（m°，n°）叫做点P 的“双角坐标”．例如，点（1，1）的“双角坐标”为（45°，90°）．
（1）点（ (1)/(2)， (√(3))/(2)）的“双角坐标”为___；
（2）若点P到x轴的距离为 (1)/(2)，则m+n的最小值为___．

Answer 1

（1）∵P（(1)/(2)，(√(3))/(2)），OA=1，
∴tan∠POA=((√(3))/(2))/((1)/(2))=√(3)，tan∠PAO=((√(3))/(2))/(1-(1)/(2))=√(3)，
∴∠POA=60°，∠PAO=60°，
即点P的“双角坐标”为（60°，60°），
故答案为：（60°，60°）；

（2）根据三角形内角和定理知若要使m+n取得最小值，即∠POA+∠PAO取得最小值，
则∠OPA需取得最大值，
如图，

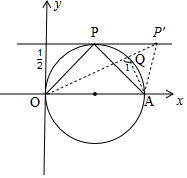
∵点P到x轴的距离为(1)/(2)，OA=1，
∴OA中点为圆心，(1)/(2)为半径画圆，与直线y=(1)/(2)相切于点P，
在直线y=(1)/(2)上任取一点P′，连接P′O、P′A，P′O交圆于点Q，
∵∠OPA=∠1>∠OP′A，
此时∠OPA最大，∠OPA=90°，
∴m+n的最小值为90，
故答案为：90．