早教吧作业答案频道 -->数学-->
在平面直角坐标系中,已知点A(-2,0),B(2,0),C(3,5).(1)求过点A,C的直线解析式和过点A,B,C的抛物线的解析式;(2)求过点A,B及抛物线的顶点D的P的圆心P的坐标;(3)在
题目详情
在平面直角坐标系中,已知点A(-2,0),B(2,0),C(3,5).
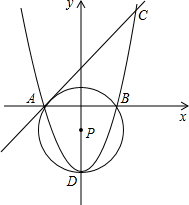
(1)求过点A,C的直线解析式和过点A,B,C的抛物线的解析式;
(2)求过点A,B及抛物线的顶点D的 P的圆心P的坐标;
(3)在抛物线上是否存在点Q,使AQ与 P相切,若存在请求出Q点坐标.

(1)求过点A,C的直线解析式和过点A,B,C的抛物线的解析式;
(2)求过点A,B及抛物线的顶点D的 P的圆心P的坐标;
(3)在抛物线上是否存在点Q,使AQ与 P相切,若存在请求出Q点坐标.
▼优质解答
答案和解析
 (1)∵A(-2,0),B(2,0);
(1)∵A(-2,0),B(2,0);
∴设二次函数的解析式为y=a(x-2)(x+2)…①,
把C(3,5)代入①得a=1;
∴二次函数的解析式为:y=x2-4;
设一次函数的解析式为:y=kx+b(k≠0)…②
把A(-2,0),C(3,5)代入②得
,
解得
,
∴一次函数的解析式为:y=x+2;
(2)设P点的坐标为(0,Py),
由(1)知D点的坐标为(0,-4);
∵A,B,D三点在 P上;
∴PB=PD;
∴22+Py2=(-4-Py)2,
解得:Py=-
;
∴P点的坐标为(0,-
);
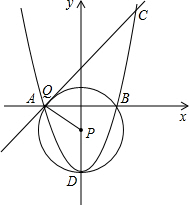
(3)在抛物线上存在这样的点Q使直线AQ与 P相切.
理由如下:设Q点的坐标为(m,m2-4);
根据平面内两点间的距离公式得:AQ2=(m+2)2+(m2-4)2,PQ2=m2+(m2-4+
)2;
∵AP=
,
∴AP2=
;
∵直线AQ是 P的切线,
∴AP⊥AQ;
∴PQ2=AP2+AQ2,
即:m2+(m2-4+
)2=
+[(m+2)2+(m2-4)2]
解得:m1=
,m2=-2(与A点重合,舍去)
∴Q点的坐标为(
,
).
 (1)∵A(-2,0),B(2,0);
(1)∵A(-2,0),B(2,0);∴设二次函数的解析式为y=a(x-2)(x+2)…①,
把C(3,5)代入①得a=1;
∴二次函数的解析式为:y=x2-4;
设一次函数的解析式为:y=kx+b(k≠0)…②
把A(-2,0),C(3,5)代入②得
|
解得
|
∴一次函数的解析式为:y=x+2;
(2)设P点的坐标为(0,Py),
由(1)知D点的坐标为(0,-4);
∵A,B,D三点在 P上;
∴PB=PD;
∴22+Py2=(-4-Py)2,
解得:Py=-
| 3 |
| 2 |
∴P点的坐标为(0,-
| 3 |
| 2 |
(3)在抛物线上存在这样的点Q使直线AQ与 P相切.
理由如下:设Q点的坐标为(m,m2-4);
根据平面内两点间的距离公式得:AQ2=(m+2)2+(m2-4)2,PQ2=m2+(m2-4+
| 3 |
| 2 |
∵AP=
| 5 |
| 2 |
∴AP2=
| 25 |
| 4 |
∵直线AQ是 P的切线,
∴AP⊥AQ;
∴PQ2=AP2+AQ2,
即:m2+(m2-4+
| 3 |
| 2 |
| 25 |
| 4 |
解得:m1=
| 10 |
| 3 |
∴Q点的坐标为(
| 10 |
| 3 |
| 64 |
| 9 |
看了 在平面直角坐标系中,已知点A...的网友还看了以下:
(1)三角形的一个顶点A的位置在(,).(2)三角形的顶点B在顶点A的正北方3cm处,位置在(,) 2020-05-02 …
已知平行四边形ABCD的三个顶点A,B,C的坐标分别为(0,1),(2,1),(-1,3),试求顶 2020-05-13 …
1.已知平行四边形ABCD的三个顶点A,B,C的坐标分别为(-2,1),(-1,3),(3,4), 2020-05-13 …
【急】在平面直角坐标系中,△ABC的两个顶点A与B在x轴上运动,且AB=2,顶点C的坐标C(0,根 2020-05-15 …
已知F、B分别为椭圆的右焦点和下顶点,A为该椭圆右准线上一点,且向量FA=-2向量FB,已知F、B 2020-05-17 …
1在△ABC中,角A,B,C所对的边分别为a,b,c,若∠C=120度,c=根号2倍a,则b/a= 2020-06-04 …
已知椭圆x^2/a^2加y^2/b^2=1(a>b>0)的左右焦点分别为F1,F2其右准线L与x轴 2020-06-30 …
如图,在正四棱锥S-ABCD中,高SO=a,底面边长为2a,求:(1)侧面与底面夹角;(2)顶点A 2020-07-31 …
如图1,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m 2020-11-01 …
(2011•富源县模拟)(1)三角形的一个顶点A的位置在(,).(2)三角形的顶点B在顶点A的正北方 2021-01-12 …