定义：对于一个函数，如果它的自变量x与函数值y满足：当m≤x≤n，有m≤y≤n，我们就称此函数是在[m，n]范围内的“标准函数．”例如：函数y=-x+4，当x=1时，y=3；当x=3时，y=1，即当1≤x≤3时

Question

定义：对于一个函数，如果它的自变量x与函数值y满足：当m≤x≤n，有m≤y≤n，我们就称此函数是在[m，n]范围内的“标准函数．”例如：函数y=-x+4，当x=1时，y=3；当x=3时，y=1，即当1≤x≤3时，有1≤y≤3，所以说函数y=-x+4是在[1，3]范围内的“标准函数．”

（1）正比例函数y=x是在[1，2015]范围内的“标准函数”吗？请判断并说明理由；
（2）若一次函数y=kx+b（k≠0）是在[2，6]范围内的“标准函数”，求此函数的解析式；
（3）如图，矩形ABCD的边长AB=2，BC=1，且B点坐标为（2，2），若一次函数y=kx+b（k<0）是在[m，n]范围的“标准函数”，当直线y=kx+b与矩形ABCD有公共点时，求m+n的最大值；
（4）在（3）的条件下，若直线y=kx+b与矩形ABCD没有公共点时，求m+n的取值范围．

Answer 1

（1）正比例函数y=x是在[1，2015]范围内的“标准函数”，理由如下：
当x=1时，y=1；当x=2015时，y=2015．
即当1≤x≤2015时，有1≤y≤2015，
∴函数y=x是在[1，2015]范围内的“标准函数”．
（2）当k>0时，有

2k+b=2

6k+b=6

，
解得：

k=1

b=0

，
∴此函数的解析式为y=x；
当k<0时，有

2k+b=6

6k+b=-2

，
解得：

k=-2

b=10

，
∴此函数的解析式为y=-2x+10．
综上可知：若一次函数y=kx+b（k≠0）是在[2，6]范围内的“标准函数”，则该函数的解析式为y=x或y=-2x+10．
（3）∵一次函数y=kx+b（k<0）是在[m，n]范围的“标准函数”，
∴

mk+b=n

nk+b=m

，解得：k=-1，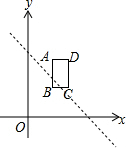
∴m+n=b，
∴一次函数的解析式为y=-x+（m+n）．
∵矩形ABCD的边长AB=2，BC=1，且B点坐标为（2，2），
∴D点的坐标为（3，4）．
当点B在该一次函数图象上时，有2=-2+（m+n），
解得：m+n=4；
当点D在该一次函数图象上时，有4=-3+（m+n），
解得：m+n=7．
∴当直线y=kx+b与矩形ABCD有公共点时，m+n的取值范围为4≤m+n≤7，
∴当直线y=kx+b与矩形ABCD有公共点时，m+n的最大值为7．
（4）由（3）可知：直线y=kx+b与矩形ABCD有公共点时，4≤m+n≤7，
∴若直线y=kx+b与矩形ABCD没有公共点时，m+n的取值范围为m+n<4或m+n>7．