从某小区随机抽取40个家庭，收集了这40个家庭去年的月均用水量（单位：吨）的数据，整理得到频数分布表和频率分布直方图．分组频数[2，4）2[4，6）10[6，8）16[8，10）8[10，12]4合计40（1）

Question

从某小区随机抽取40个家庭，收集了这40个家庭去年的月均用水量（单位：吨）的数据，整理得到频数分布表和频率分布直方图．

分组	频数
[2，4）	2
[4，6）	10
[6，8）	16
[8，10）	8
[10，12]	4
合计	40

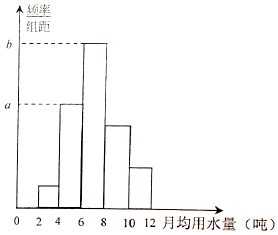
（1）求频率分布直方图中a，b的值；
（2）从该小区随机选取一个家庭，试估计这个家庭去年的月均用水量不低于6吨的概率；
（3）在这40个家庭中，用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本，将该样本看成一个总体，从中任意选取2个家庭，求其中恰有一个家庭的月均用水量不低于8吨的概率．

Answer 1

（1）因为样本中家庭月均用水量在[4，6）上的频率为(10)/(40)=0.25，
在[6，8）上的频率为(16)/(40)=0.4，
所以a=(0.25)/(2)=0.125，b=(0.4)/(2)=0.2．
（2）根据频数分布表，40个家庭中月均用水量不低于6吨的家庭共有28个，
所以样本中家庭月均用水量不低于6吨的概率是(28)/(40)=0.7，
利用样本估计总体，从该小区随机选取一个家庭，可估计这个家庭去年的月均用水量不低于6吨的概率约为0.7．
（3）在这40个家庭中，用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本，
则在[6，8）上应抽取7×(16)/(28)=4人，记为A，B，C，D，
在[8，10）上应抽取7×(8)/(28)=2人，记为E，F，
在[10，12）上应抽取7×(4)/(28)=1人，记为G．
从中任意选取2个家庭的所有基本事件有：（A，B），（A，C），（A，D），（A，E），（A，F），（A，G），（B，C），（B，D），（B，E），（B，F），（B，G），（C，D），（C，E），（C，F），（C，G），（D，E），（D，F），（D，G），（E，F），（E，G），（F，G），共21种．
其中恰有一个家庭的月均用水量不低于8吨的事件有：（A，E），（A，F），（A，G），（B，E），（B，F），（B，G），（C，E），（C，F），（C，G），（D，E），（D，F），（D，G），共12种．
所以其中恰有一个家庭的月均用水量不低于8吨的概率为(12)/(21)=(4)/(7)．