早教吧作业答案频道 -->数学-->
如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;(2)若正方形ABCD的边长为1,∠AG
题目详情
如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
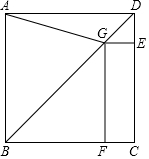
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.

(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
▼优质解答
答案和解析
(1)结论:AG2=GE2+GF2.
理由:连接CG.
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,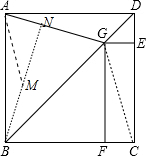
∴CF=GE,
在Rt△GFC中,∵CG2=GF2+CF2,
∴AG2=GF2+GE2.
(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.
∵∠AGF=105°,∠FBG=∠FGB=∠ABG=45°,
∴∠AGB=60°,∠GBN=30°,∠ABM=∠MAB=15°,
∴∠AMN=30°,
∴AM=BM=2x,MN=
x,
在Rt△ABN中,∵AB2=AN2+BN2,
∴1=x2+(2x+
x)2,
解得x=
,
∴BN=
,
∴BG=BN÷cos30°=
.
理由:连接CG.
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,

∴CF=GE,
在Rt△GFC中,∵CG2=GF2+CF2,
∴AG2=GF2+GE2.
(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.
∵∠AGF=105°,∠FBG=∠FGB=∠ABG=45°,
∴∠AGB=60°,∠GBN=30°,∠ABM=∠MAB=15°,
∴∠AMN=30°,
∴AM=BM=2x,MN=
| 3 |
在Rt△ABN中,∵AB2=AN2+BN2,
∴1=x2+(2x+
| 3 |
解得x=
| ||||
| 4 |
∴BN=
| ||||
| 4 |
∴BG=BN÷cos30°=
3
| ||||
| 6 |
看了 如图,在正方形ABCD中,点...的网友还看了以下:
如图,已知一条直线经过点A(0,4)、点B(2,0),点A关于x轴的对称点为D点B关于y轴的对称点 2020-05-02 …
对于密闭容器中的反应:N2(g)+3H2(g)=2NH3(g)在673K,30MPa下n(NH3) 2020-05-13 …
已知椭圆C:+=1(a>b>0)的焦距为4,且过点P(,).(1)求椭圆C的方程;(2)设Q(x0 2020-05-15 …
如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形 2020-05-16 …
如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形 2020-05-16 …
如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形 2020-07-29 …
已知A(1,0),点B在曲线G:y=ln(x+1)上,若线段AB与曲线M:y=1x相交且交点恰为线 2020-07-30 …
已知:如图,在三角形ABC中,D、E分别是边AB、AC的中点,AB的垂线过点D交AC于点F,AC的 2020-08-01 …
D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC内任意一点, 2020-08-03 …
关于自由落体加速度g,下列说法正确的是()A.同一物体不论什么地点g相等B.重的物体与轻的物体相比较 2021-01-22 …