早教吧作业答案频道 -->数学-->
D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC内任意一点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.问当OA与BC应满足怎样的数量关系时,四边形
题目详情
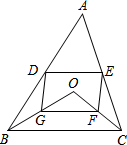
D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC内任意一点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.问当OA与BC应满足怎样的数量关系时,四边形DGFE是菱形,并证明之.

▼优质解答
答案和解析
当OA=BC时,四边形DEFG是菱形.
理由:∵D、E分别是AB、AC的中点,
∴DE∥BC,DE=
BC,
同理,GF∥BC,FG=
BC,
∴DE∥FG,DE=GF,
∴四边形DEFG是平行四边形,
连接OA,在△AOC中,E、F分别为AC、OC中点,
∴EF=
OA,同理在△BOC中,GF=
BC,
∵OA=BC,
∴EF=GF,
∴OA=BC时,四边形DEFG是菱形.
理由:∵D、E分别是AB、AC的中点,

∴DE∥BC,DE=
| 1 |
| 2 |
同理,GF∥BC,FG=
| 1 |
| 2 |
∴DE∥FG,DE=GF,
∴四边形DEFG是平行四边形,
连接OA,在△AOC中,E、F分别为AC、OC中点,
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
∵OA=BC,
∴EF=GF,
∴OA=BC时,四边形DEFG是菱形.
看了 D、E分别是不等边三角形AB...的网友还看了以下:
定义在R上的奇函数f(x)是增函数,偶函数g(x)在区间零到正无穷左闭右开上的图像与f(x)的图像重 2020-03-31 …
已知f(X)=Lg1-X/1+X,a,b属于(-1,1)求证:f(a)+f(B)=F(A+B)/1 2020-05-22 …
定义在R上的函数y=f(x),满足f(x+2)=-1/f(x),则().A.f(x)不是周期函数B 2020-06-03 …
高数题目设f(x)在[a,b]上可导,又f'(x)+[f(x)]^2-∫(a到x)f(t)dt=0 2020-06-12 …
设函数f(x)在点x0及其邻近有定义,且有f(x0+Δx)-f(x0)=aΔx+b(Δx)^2.a 2020-07-22 …
5道比较简单的大一积分题1.设函数f(x)在[a,b]上具有连续的导函数,且f(a)=f(b)=0 2020-07-28 …
1、已知f(x)=3的x次方,求证:(1)、f(x)乘以f(y)=f(x+y)(2)、f(x)除以 2020-07-30 …
已知f(x),g(x)都是奇函数f(x)>0的x∈(a,b),g(x)>0的解集是x∈(a/2,b 2020-07-30 …
f(a)+f(b)=2f[(a+b)/2]*f[(a-b)/2]的奇偶性已知函数f(x)对于任意实 2020-08-01 …
设f(x)在[a,b]连续,在(a,b)二阶可导,连接点A(a,f(a))和B(b,f(b))的直线 2020-12-28 …