早教吧作业答案频道 -->数学-->
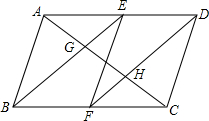
如图,在▱ABCD中,E、F分别为边AD、BC的中点,对角线AC分别交BE,DF于点G、H.求证:AG=CH.
题目详情
如图,在▱ABCD中,E、F分别为边AD、BC的中点,对角线AC分别交BE,DF于点G、H.求证:AG=CH.

▼优质解答
答案和解析
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADF=∠CFH,∠EAG=∠FCH,
∵E、F分别为AD、BC边的中点,
∴AE=DE=
AD,CF=BF=
BC,
∴DE∥BF,DE=BF,
∴四边形BFDE是平行四边形,
∴BE∥DF,
∴∠AEG=∠ADF,
∴∠AEG=∠CFH,
在△AEG和△CFH中,
,
∴△AEG≌△CFH(ASA),
∴AG=CH.
∴AD∥BC,
∴∠ADF=∠CFH,∠EAG=∠FCH,
∵E、F分别为AD、BC边的中点,
∴AE=DE=
| 1 |
| 2 |
| 1 |
| 2 |
∴DE∥BF,DE=BF,
∴四边形BFDE是平行四边形,
∴BE∥DF,
∴∠AEG=∠ADF,
∴∠AEG=∠CFH,
在△AEG和△CFH中,
|
∴△AEG≌△CFH(ASA),
∴AG=CH.
看了 如图,在▱ABCD中,E、F...的网友还看了以下:
1.log89=a,log35=b,用a,b表示lg22.log155*log1545+(log1 2020-05-13 …
O、A、B、C为空间四个点,又OA、OB、OC为空间的一个基底,则()A.O、A、B、C四点不共线 2020-05-14 …
因式分解a3(b-c)+b3(c-a)+c3(a-b)如果用待定系数法解,得a3(b-c)+b3( 2020-05-16 …
1.已知a,b,c为△ABC的边,且满足a²(c²-a²)=b²(c²-b²),试判断此三角形的形 2020-06-05 …
阅读下题的解题过程:已知a、b、c为三角形ABC的三边,且满足a^2c^2-b^2c^2=a^4- 2020-06-08 …
第一题令A={a,b,c,d,e},B={a,b,c,d,e,f,g,h}.求a)A∪Bb)A∩B 2020-06-17 …
在锐角三角形ABC中,角A,B,C的对边分别为a,b,c.已知sin(A-B)=cosC.(1)求 2020-07-30 …
用C(A)表示非空集合A中的元素个数,定义A*B=C(A)-C(B),当C(A)≥C(B)C(B) 2020-08-01 …
1.设a,b,c为int型变量,且a=3,b=4,c=5,下面表达式值为0的是(ABCD).A.'a 2020-10-30 …
求绿地面积A,B,C为坐落在一条南北走向的公路沿线上的三个汽车站,其中AB、BC的距离分别为3千米和 2020-11-21 …