（本小题满分12分）已知等比数列{an}的前n项和An=，数列{bn}(bn＞0)的首项为b1=a，且前n项和Sn满足Sn-Sn-1=；（1）求数列{an}和{bn}的通项公式；（2）若数列

Question

（本小题满分12分）

已知等比数列{a _n }的前n项和A _n = 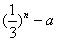，数列{b _n }(b _n ＞0)的首项为b ₁ =a，且前n项和S _n 满足S _n -S _n-1 = ；

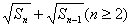（1）求数列{a _n }和{b _n }的通项公式；

（2）若数列 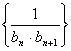的前n项和为T _n ，判断T _n +a _n (b _n +1)与0的大小。

Answer 1

（1）a1=–a，a2=A2–A1= –，a3=A3–A2=–， 又数列{an}成等比数列，∴ a22=a1a3，即=(–a)∙( –)∴a=1，又公比q== ∴an== –2 ∵Sn-Sn-1= 又bn＞0，数列{}是首相为1，公差为1的等差数列， 当n=1时，b1=1；当n≥2时，bn=Sn–Sn-1=n2-(n-1)2=2n-1 所以bn=2n-1。 Tn+an(bn+1)=-2n´2()n= 当n=1 、2、3时，Tn+an(bn+1)<0， 当n≥4时，Tn+an(bn+1)>0，即n≥4时，3n>4(2n+1)，下用数学归纳法证明： 当n=4时，34=81，而4（2´4+1）=36，∴n=4时，3n>4(2n+1)。 假设n=k(k≥4)时，不等式成立，即：； 则n=k+1时，3k+1>3´4(2k+1)=4(6k+3)>4(2k+3)=4[2(k+1)+1]，即：n=k+1时，不等式成立。 综上可知：n≥4时，3n>4(2n+1)。 故当n=1 、2、3时，Tn+an(bn+1)<0； 当n≥4时，3n>4(2n+1)。