已知双曲线C：x2a2-y2b2=1（a>0，b>0）的左、右焦点分别为F1、F2．左、右顶点分别为A、B，虚轴的上、下端点分别为C、D．若线段BC与双曲线的渐近线的交点为E，且∠BF1E=∠CF1E，则双曲线的

Question

已知双曲线C：

(x2)/(a2)-(y2)/(b2)=1（a>0，b>0）的左、右焦点分别为F₁、F₂．左、右顶点分别为A、B，虚轴的上、下端点分别为C、D．若线段BC与双曲线的渐近线的交点为E，且∠BF₁E=∠CF₁E，则双曲线的离心率为（　　）

A. 1+

√(6)

B. 1+

√(5)

C. 1+

√(3)

D. 1+

√(2)

Answer 1

双曲线C：(x2)/(a2)-(y2)/(b2)=1（a>0，b>0）的渐近线方程为y=±(b)/(a)x，
由B（a，0），C（0，b），可得直线CB的方程为bx+ay=ab，
联立渐近线方程y=(b)/(a)x，解得E（(a)/(2)，(b)/(2)），
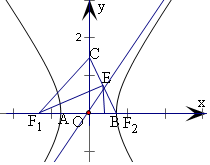
即有E为CB的中点，
由∠BF₁E=∠CF₁E，
即F₁E平分∠CF₁B，
可得三角形CF₁B为等腰三角形，
即有CF₁=BF₁，即√(b2+c2)=a+c，
又a²+b²=c²，可得c²=2a²+2ac，
由e=(c)/(a)，可得e²-2e-2=0，
解得e=1+√(3)．
故选：C．