已知在双曲线x2a2-y2b2=1中，F1，F2分别是左右焦点，A1，A2，B1，B2分别为双曲线的实轴与虚轴端点，若以A1A2为直径的圆总在菱形F1B1F2B2的内部，则此双曲线x2a2-y2b2=1离心率的取值范围是（）

Question

已知在双曲线

(x2)/(a2)-(y2)/(b2)=1中，F₁，F₂分别是左右焦点，A₁，A₂，B₁，B₂分别为双曲线的实轴与虚轴端点，若以A₁A₂为直径的圆总在菱形F₁B₁F₂B₂的内部，则此双曲线(x2)/(a2)-(y2)/(b2)=1离心率的取值范围是（　　）

A. (1，

(1+√(5))/(2))

B. (

(1+√(5))/(2)，+∞)

C. (1，

(1+√(3))/(2))

D. (

(1+√(3))/(2)，+∞)

Answer 1

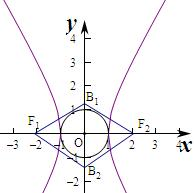双曲线F₁（-c，0），F₂（c，0），B₁（0，b），B₂（0，-b），
则圆的半径为a，
若以A₁A₂为直径的圆总在菱形F₁B₁F₂B₂的内部，
则圆心O到直线B₁F₂的距离d≥c，
直线B₁F₂的方程：(x)/(c)+(y)/(b)=1，即bx+cy-bc=0，
则d=(|bc|)/(√(b2+c2))≥a，
即b²c²≥a²（b²+c²），
即（c²-a²）c²≥a²（2c²-a²），
即c⁴-3a²c²+a⁴≥0，
即e⁴-3e²+1≥0，
即e²≥(3+√(5))/(2)或e²≤(3-√(5))/(2)（舍），
即e²≥(3+√(5))/(2)=（(1+√(5))/(2)）²，
则e≥(1+√(5))/(2)，
故选：A