早教吧作业答案频道 -->数学-->
设P为双曲线上除顶点外的任意一点，F1，F2分别为左右点，△F1PF2的内切圆交实轴于点M，则|F1M|?|MF2|值为．
题目详情
设P为双曲线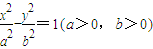
上除顶点外的任意一点，F 1 ，F 2 分别为左右点，△F 1 PF 2 的内切圆交实轴于点M，则|F 1 M|?|MF 2 |值为 ．
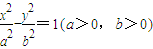上除顶点外的任意一点，F 1 ，F 2 分别为左右点，△F 1 PF 2 的内切圆交实轴于点M，则|F 1 M|?|MF 2 |值为 ．▼优质解答
答案和解析
分析：
根据图象和圆切线长定理可知|F1M|-|F2M|=±2a，与|F1M|+|MF2|=|F1F2|=2c联立即可求出|F1M|和|MF2|，|F1M|与|F2M|的积再根据双曲线的基本性质c2-a2=b2化简得到值．
由已知，得|PF1|-|PF2|=±2a，即|F1M|-|F2M|=±2a．又|F1M|+|F2M|=2c，∴|F1M|=c+a或c-a，|F2M|=c-a或c+a．因此|F1M|?|MF2|=（c+a）（c-a）=c2-a2=b2．故答案为：b2．
点评：
本小题主要考查双曲线的定义、双曲线的基本性质、圆切线长定理等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
分析：
根据图象和圆切线长定理可知|F1M|-|F2M|=±2a，与|F1M|+|MF2|=|F1F2|=2c联立即可求出|F1M|和|MF2|，|F1M|与|F2M|的积再根据双曲线的基本性质c2-a2=b2化简得到值．
由已知，得|PF1|-|PF2|=±2a，即|F1M|-|F2M|=±2a．又|F1M|+|F2M|=2c，∴|F1M|=c+a或c-a，|F2M|=c-a或c+a．因此|F1M|?|MF2|=（c+a）（c-a）=c2-a2=b2．故答案为：b2．
点评：
本小题主要考查双曲线的定义、双曲线的基本性质、圆切线长定理等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
看了 设P为双曲线上除顶点外的任意...的网友还看了以下：
若多项式f(x)=x^3+a^2x^2+x-3a能被x-1整除,则实数a=?若多项式f(x)=x^ 2020-05-13 …
设F(X),G(X)是数域K上的不可约多项式,存在C属于C,若X-C整除F(X),G(X),则G( 2020-06-03 …
一个式子若是f(x)的因式就是说它能整出f(x)吗?如题.例如(x-2)是f(x)的因式,那么(x 2020-07-05 …
关于多项式余式的问题?以x^2+2x+3除f(x)余x+12,以(x+1)^2除f(x)余5x+4 2020-07-30 …
已知，对于任意的多项式f（x）与任意复数z，f（z）=0⇔x-z整除f（x）．利用上述定理解决下列 2020-08-02 …
关于需要向心力与实际提供向心力的辨析关于火车转弯问题当v.>v0时轨道对外侧轮缘有挤压因为v增大导致 2020-10-30 …
如何证明如果(x1)整除f(xN)那么(xN1)整除f(xN)如果x-1整除f(x^n),那证明x^ 2020-10-31 …
1、若数域F属于F*,当f(x),g(x)属于F(x)时,有f(x)不整除g(x),则在F(x)*内 2020-11-20 …
如果p(x)是不可约多项式,那么对于任意的两个多项式f(x),g(x),由p(x)|f(x)g(x) 2020-12-28 …
在做“探究力的平行四边形定则”实验中，若由于F1的误差使F1与F2的合力F方向略向左偏，如图实－2－ 2021-01-02 …