早教吧作业答案频道 -->数学-->
在平面直角坐标系中,直线y=-35x+3与x轴、y轴相交于B、C两点,动点D在线段OB上,将线段DC绕着点D顺时针旋转90°得到DE,过点E作直线l⊥x轴于H,过点C作CF⊥y轴,交直线l于F,设点D的横坐标为m
题目详情
在平面直角坐标系中,直线y=-
x+3与x轴、y轴相交于B、C两点,动点D在线段OB上,将线段DC绕着点D顺时针旋转90°得到DE,过点E作直线l⊥x轴于H,过点C作CF⊥y轴,交直线l于F,设点D的横坐标为m.
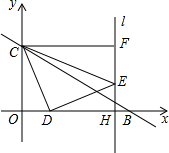
(1)请直接写出点B、C的坐标;
(2)当点E落在直线BC上时,求tan∠FDE的值;
(3)对于常数m,探究:在直线l上是否存在点G,使得∠CDO=∠DFE+∠DGH?若存在,请求出点G的坐标;若不存在,请说明理由.
| 3 |
| 5 |

(1)请直接写出点B、C的坐标;
(2)当点E落在直线BC上时,求tan∠FDE的值;
(3)对于常数m,探究:在直线l上是否存在点G,使得∠CDO=∠DFE+∠DGH?若存在,请求出点G的坐标;若不存在,请说明理由.
▼优质解答
答案和解析
 (1)∵直线y=-
(1)∵直线y=-
x+3与x轴、y轴相交于B、C两点,
∴令y=0,则0=-
x+3,解得x=5,令x=0,则y=3,
∴B(5,0),C(0,3);
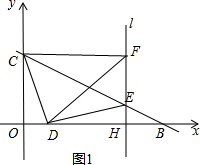
(2)如图1,∵∠CDE=90°,
∴∠CDO+∠EDH=90°,
∵∠CDO+∠OCD=90°,
∴∠OCD=∠EDH,
在△OCD和△HDE中,
,
∴△OCD≌△HDE(AAS),
∴DH=OC=3,
∵直线l⊥x轴于H,CF⊥y轴,
∴四边形COHF是矩形,
∴FH=OC=3,
∴DH=HF,
∴∠HDF=45°,即∠HDE+∠FDE=45°,
∵CD=DE,∠CDE=90°,
∴∠DCE=45°,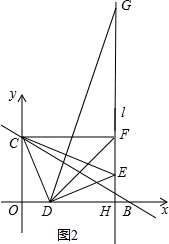
∴∠OCD+∠ECF=45°,
∴∠ECF=∠FDE,
∵∠OBC=∠ECF,
∵tan∠OBC=
=
,
∴tan∠FDE=
.
(3)如图2,由(2)可知△OCD≌△HDE,
∴∠CDO=∠DEH,
要使∠CDO=∠DFE+∠DGH,只要∠DEH=∠DFE+∠DGH,
在△DEF中,∠DEH=∠EDF+∠DFE,
∴只要∠EDF=∠DGF,
∵∠FED=∠GED,
只要△EDF∽△EGD,
∴只要
=
,即DE2=EF•EG,
由(2)可知:DE2=CD2=OD2+OC2=m2+32,EF=3-m,
∴当0<m<3时,EG=
+m=
,HO=3+m,
此时,G(3+m,
),
根据对称可知,当0<m<3时,此时还存在G′(3+m,-
);
当m=3时,此时点E和点F重合,∠DFE不存在,
当3≤m≤5时,点E在F的上方,此时,∠DFE>∠DEF,
此时不存在∠CDO=∠DFE+∠DGH,
综上,当0<m<3时,存在∠CDO=∠DFE+∠DGH,此时G(3+m,
)或(3+m,-
).
 (1)∵直线y=-
(1)∵直线y=-| 3 |
| 5 |
∴令y=0,则0=-
| 3 |
| 5 |
∴B(5,0),C(0,3);
(2)如图1,∵∠CDE=90°,
∴∠CDO+∠EDH=90°,
∵∠CDO+∠OCD=90°,
∴∠OCD=∠EDH,
在△OCD和△HDE中,
|
∴△OCD≌△HDE(AAS),
∴DH=OC=3,
∵直线l⊥x轴于H,CF⊥y轴,
∴四边形COHF是矩形,
∴FH=OC=3,
∴DH=HF,
∴∠HDF=45°,即∠HDE+∠FDE=45°,
∵CD=DE,∠CDE=90°,
∴∠DCE=45°,

∴∠OCD+∠ECF=45°,
∴∠ECF=∠FDE,
∵∠OBC=∠ECF,
∵tan∠OBC=
| OC |
| OB |
| 3 |
| 5 |
∴tan∠FDE=
| 3 |
| 5 |
(3)如图2,由(2)可知△OCD≌△HDE,
∴∠CDO=∠DEH,
要使∠CDO=∠DFE+∠DGH,只要∠DEH=∠DFE+∠DGH,
在△DEF中,∠DEH=∠EDF+∠DFE,
∴只要∠EDF=∠DGF,
∵∠FED=∠GED,
只要△EDF∽△EGD,
∴只要
| EF |
| DE |
| DE |
| EG |
由(2)可知:DE2=CD2=OD2+OC2=m2+32,EF=3-m,
∴当0<m<3时,EG=
| m2+9 |
| 3-m |
| 9+3m |
| 3-m |
此时,G(3+m,
| 9+3m |
| 3-m |
根据对称可知,当0<m<3时,此时还存在G′(3+m,-
| 9+3m |
| 3-m |
当m=3时,此时点E和点F重合,∠DFE不存在,
当3≤m≤5时,点E在F的上方,此时,∠DFE>∠DEF,
此时不存在∠CDO=∠DFE+∠DGH,
综上,当0<m<3时,存在∠CDO=∠DFE+∠DGH,此时G(3+m,
| 9+3m |
| 3-m |
| 9+3m |
| 3-m |
看了 在平面直角坐标系中,直线y=...的网友还看了以下:
有关于直角坐标系D是正方形OABC的边OC上一点,作∠BAD的平分线交BC与点E,延长CO到F,使 2020-05-13 …
二次函数的顶点坐标,交点坐标横纵坐标都是怎么求的?要式子, 2020-05-13 …
双曲线Y=5/X在第一象限的一分支上有一点C(1.5),过点C的直线CA:Y=KX+B与X轴相交于 2020-06-04 …
如图所示,双曲线y=kx,在第一象限的一支上有一点C(1,5),经过点C的直线y=-kx+b(k> 2020-07-26 …
反比例函数经过点A,B,点A(1,3)点B横坐标是3,点C是X轴上的一个动点直线BC和反比例函数的 2020-08-01 …
平面直角坐标系中,A(-4,0),B(0,2),C(6,0),直线AB与直线CD交于D,D点横纵坐 2020-08-01 …
设a,b∈R,c∈[0,2π),若对任意实数x都有2sin(3x-π3)=asin(bx+c),定 2020-08-03 …
双曲线Y=5/X在第一象限的一支上有一点C(1,5)过点C的直线Y=—kx+b(k>0)与X轴交于点 2020-11-08 …
双曲线y=5/x在第一象限的一支上有一点C(1,5),过点C的直线y=kx+b(k>0)与x轴交与点 2020-12-03 …
RT△OAB其中角AOB=90°OA=2OB=4将它放置在坐标系中折叠折痕与OB交点C与边AB交点D 2020-12-25 …