早教吧作业答案频道 -->数学-->
如图,∠CBF、∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC、∠CBF的平分线BD、BE交于点D、E.(1)求∠DBE的度数;(2)若∠A=70°,求∠D的度数;(3)若∠A=a,则∠D=,∠E=
题目详情
如图,∠CBF、∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC、∠CBF的平分线BD、BE交于点D、E.
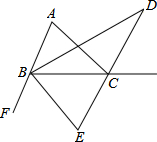
(1)求∠DBE的度数;
(2)若∠A=70°,求∠D的度数;
(3)若∠A=a,则∠D=___,∠E=___(用含a的式子表示)

(1)求∠DBE的度数;
(2)若∠A=70°,求∠D的度数;
(3)若∠A=a,则∠D=___,∠E=___(用含a的式子表示)
▼优质解答
答案和解析
(1)∵BD平分∠ABC,BE平分∠CBF,
∴∠DBC=
∠ABC,∠CBE=
∠CBF,
∴∠DBC+∠CBE=
(∠ABC+∠CBF)=90°,
∴∠DBE=90°;
(2)∵CD平分∠ACG,BD平分∠ABC,
∴∠DCG=
∠ACG,∠DBC=
∠ABC,
∵∠ACD=∠A+∠ABC,
∴2∠DCG=∠ACF=∠A+∠ABC=∠A+2∠DBC,
∵∠DCG=∠D+∠DBC,
∴2∠DCG=2∠D+2∠DBC,
∴∠A+2∠DBC=2∠D+2∠DBC,
∴∠D=
∠A=35°;
(3)由(2)知∠D=
∠A,
∵∠A=α,
∴∠D=
α,
∵∠DBE=90°,
∴∠E=90°-
α.
故答案为:
α,90°-
α.
∴∠DBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DBC+∠CBE=
| 1 |
| 2 |
∴∠DBE=90°;
(2)∵CD平分∠ACG,BD平分∠ABC,
∴∠DCG=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ACD=∠A+∠ABC,
∴2∠DCG=∠ACF=∠A+∠ABC=∠A+2∠DBC,
∵∠DCG=∠D+∠DBC,
∴2∠DCG=2∠D+2∠DBC,
∴∠A+2∠DBC=2∠D+2∠DBC,
∴∠D=
| 1 |
| 2 |
(3)由(2)知∠D=
| 1 |
| 2 |
∵∠A=α,
∴∠D=
| 1 |
| 2 |
∵∠DBE=90°,
∴∠E=90°-
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
| 1 |
| 2 |
看了 如图,∠CBF、∠ACG是△...的网友还看了以下:
在平行四边形ABCD中,点E,F分别是线段AD,BC上的两动点,点E从点A向D运动在平行四边形AB 2020-05-13 …
在三角形ABC中,CD,BE是外角的平分线,BD,CE是内角的平分线,BE,CE相交于E点,角E= 2020-05-13 …
几个初一的数学题(急)关于三角形的外角1.在三角形ABC中,角B的平分线与角BAC的外角平分线相交 2020-05-14 …
运动粒子在复合场中做功情况比较一个重力不计的带电粒子以水平初速度V0(V0小于E/B)先后穿过宽度 2020-05-20 …
在△ABC中∠ABC的平分线和∠ACD的平分线相交于点E且∠A=60°求∠E的度数 2020-06-07 …
如图,在△ABC中,AD平分∠BAC,P为线段AD上一个动点,PE⊥AD交直线BC于点E①若∠B= 2020-06-27 …
在三角形BCD中,BE平分角DBC交CD于F,延长BC至G,CE平分角DCG,且EC.DB的延长线 2020-07-17 …
相同温度,分子的平均速度相同么?类似的问题上述的.质量相同,温度相同的氧气和氢气分子平均速度相同? 2020-07-22 …
三棱柱ABC-A1B1C1的侧棱垂直于底面,且底面ABC在平行四边形ACDE所在的平面内,AE=2 2020-07-31 …
AD是三角形ABC中角BAC的平分线,AE是三角形ABC的外角平分线交BC延长线于E且角BAD=2 2020-08-03 …