早教吧作业答案频道 -->数学-->
用两种方法证明“直角三角形斜边上的中线等于斜边的一半”.已知:如图1,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.求证:CD=12AB.证法1:如图2,在∠ACB的内部
题目详情
用两种方法证明“直角三角形斜边上的中线等于斜边的一半”.
已知:如图1,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD=
AB.
证法1:如图2,在∠ACB的内部作∠BCE=∠B,
CE与AB相交于点E.
∵∠BCE=∠B,
∴___.
∵∠BCE+∠ACE=90°,
∴∠B+∠ACE=90°.
又∵___,
∴∠ACE=∠A.
∴EA=EC.
∴EA=EB=EC,
即CE是斜边AB上的中线,且CE=
AB.
又∵CD是斜边AB上的中线,即CD与CE重合,
∴CD=
AB.
请把证法1补充完整,并用不同的方法完成证法2.
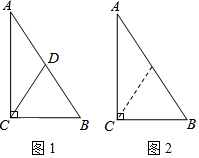
已知:如图1,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD=
| 1 |
| 2 |
证法1:如图2,在∠ACB的内部作∠BCE=∠B,
CE与AB相交于点E.
∵∠BCE=∠B,
∴___.
∵∠BCE+∠ACE=90°,
∴∠B+∠ACE=90°.
又∵___,
∴∠ACE=∠A.
∴EA=EC.
∴EA=EB=EC,
即CE是斜边AB上的中线,且CE=
| 1 |
| 2 |
又∵CD是斜边AB上的中线,即CD与CE重合,
∴CD=
| 1 |
| 2 |
请把证法1补充完整,并用不同的方法完成证法2.

▼优质解答
答案和解析
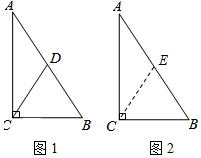 证法1:如图2,在∠ACB的内部作∠BCE=∠B,
证法1:如图2,在∠ACB的内部作∠BCE=∠B,
CE与AB相交于点E.
∵∠BCE=∠B,
∴EC=EB,
∵∠BCE+∠ACE=90°,
∴∠B+∠ACE=90°.
又∵∠A+∠B=90°,
∴∠ACE=∠A.
∴EA=EC.
∴EA=EB=EC,
即CE是斜边AB上的中线,且CE=
AB.
又∵CD是斜边AB上的中线,即CD与CE重合,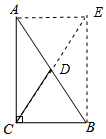
∴CD=
AB.
故答案为:EC=EB;∠A+∠B=90°;
证法2:延长CD至点E,使得DE=CD,连接AE、BE.如图3所示:
∵AD=DB,DE=CD.
∴四边形ACBE是平行四边形.
又∵∠ACB=90°,
∴四边形ACBE是矩形.
∴AB=CE,
又∵CD=
CE,
∴CD=
AB.
 证法1:如图2,在∠ACB的内部作∠BCE=∠B,
证法1:如图2,在∠ACB的内部作∠BCE=∠B,CE与AB相交于点E.
∵∠BCE=∠B,
∴EC=EB,
∵∠BCE+∠ACE=90°,
∴∠B+∠ACE=90°.
又∵∠A+∠B=90°,
∴∠ACE=∠A.
∴EA=EC.
∴EA=EB=EC,
即CE是斜边AB上的中线,且CE=
| 1 |
| 2 |
又∵CD是斜边AB上的中线,即CD与CE重合,

∴CD=
| 1 |
| 2 |
故答案为:EC=EB;∠A+∠B=90°;
证法2:延长CD至点E,使得DE=CD,连接AE、BE.如图3所示:
∵AD=DB,DE=CD.
∴四边形ACBE是平行四边形.
又∵∠ACB=90°,
∴四边形ACBE是矩形.
∴AB=CE,
又∵CD=
| 1 |
| 2 |
∴CD=
| 1 |
| 2 |
看了 用两种方法证明“直角三角形斜...的网友还看了以下:
Rt三角形的斜边上的中线等于斜边的一半证法Rt三角形的斜边上的中线等于斜边的一半有什么证法,Who 2020-04-26 …
已知Rt△ABC的周长是4+4根号3,斜边上的中线长是2,则S△ABC=?设两条直角边为x、y.因 2020-05-14 …
直角三角形斜边中点,中点到直角的连线,等于斜边的一半,怎么证明直角三角形直角到斜边中点=斜边一半? 2020-05-14 …
下列说法,不正确的是()A一组邻边相等的平行四边形是菱形B等腰直角三角形斜边上的高等于斜边的一半C 2020-06-03 …
是关与三角涵数的,一个三角形,直角边a与斜边b夹角为10度,直角边长7.5,求斜边b和另一斜边c长 2020-06-29 …
直角三角形中斜边上一点和直角边交点的连线的长度(即斜边上的中线)为斜边的一半则这个点是斜边的中点这 2020-07-21 …
性质3:在直角三角形中,斜边上的中线等于斜边的一半(即直角三角形的外心位于斜边的中点,外接圆半径R 2020-07-30 …
命题判断下列命题中,不正确的是A.对角线相等的平行四边形是矩形B.有一个角为60°的等腰三角形是等 2020-08-01 …
请问数学几何中有这个定理吗:直角三角形斜边上的高等于斜边的一半?注意是:斜边的高,不是斜边的中线谢 2020-08-01 …
直角三角形斜边中线等于斜边的一半这个定理能逆用吗?斜边的一半等于斜边中线能证三角形是直角三角形吗? 2020-11-10 …