早教吧作业答案频道 -->数学-->
在Rt△ABC中,∠C=90°,AC=6,点D是斜边AB中点,作DE⊥AB,交直线AC于点E.(1)若∠A=30°,求线段CE的长;(2)当点E在线段AC上时,设BC=x,CE=y,求y关于x的函数解析式,并写出定义域;(3)
题目详情
在Rt△ABC中,∠C=90°,AC=6,点D是斜边AB中点,作DE⊥AB,交直线AC于点E.
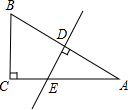
(1)若∠A=30°,求线段CE的长;
(2)当点E在线段AC上时,设BC=x,CE=y,求y关于x的函数解析式,并写出定义域;
(3)若CE=1,求BC的长.

(1)若∠A=30°,求线段CE的长;
(2)当点E在线段AC上时,设BC=x,CE=y,求y关于x的函数解析式,并写出定义域;
(3)若CE=1,求BC的长.
▼优质解答
答案和解析
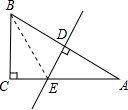 (1)连接BE,点D是AB中点且DE⊥AB,
(1)连接BE,点D是AB中点且DE⊥AB,
∵∠A=30°,∴∠ABC=90°-30°=60°,
又∵DE垂直平分AB,
∴∠ABE=∠BAE=30°,∠CBE=∠ABC-∠ABE=30°,
又∵∠C=90°,∴CE=
BE=
AE,
∵AC=6,∴BE=AE=4,CE=
BE=
×4=2
答:线段CE的长为2;
(2)连接BE,则AE=BE=6-y,
在Rt△BCE中,由勾股定理得BC2+CE2=BE2,即x2+y2=(6-y)2,
解得y=3-
,
得y=3-
≥0,解得(0<x≤6)
答:y关于x的函数解析式是y=3-
;定义域是0<x≤6.
(3)当点E在线段AC上时,由(2)得1=3-
,
解得x=2
(负值已舍)
当点E在AC延长线上时,AE=BE=7,
在Rt△BCE中,由勾股定理得BC2+CE2=BE2,即x2+12=72.
解得x=4
(负值已舍).
综上所述,满足条件的BC的长为2
,4
.
答:若CE=1,BC的长为2
和4
.
 (1)连接BE,点D是AB中点且DE⊥AB,
(1)连接BE,点D是AB中点且DE⊥AB,∵∠A=30°,∴∠ABC=90°-30°=60°,
又∵DE垂直平分AB,
∴∠ABE=∠BAE=30°,∠CBE=∠ABC-∠ABE=30°,
又∵∠C=90°,∴CE=
| 1 |
| 2 |
| 1 |
| 2 |
∵AC=6,∴BE=AE=4,CE=
| 1 |
| 2 |
| 1 |
| 2 |
答:线段CE的长为2;
(2)连接BE,则AE=BE=6-y,
在Rt△BCE中,由勾股定理得BC2+CE2=BE2,即x2+y2=(6-y)2,
解得y=3-
| x2 |
| 12 |
得y=3-
| x2 |
| 12 |
答:y关于x的函数解析式是y=3-
| x2 |
| 12 |
(3)当点E在线段AC上时,由(2)得1=3-
| x2 |
| 12 |
解得x=2
| 6 |
当点E在AC延长线上时,AE=BE=7,
在Rt△BCE中,由勾股定理得BC2+CE2=BE2,即x2+12=72.
解得x=4
| 3 |
综上所述,满足条件的BC的长为2
| 6 |
| 3 |
答:若CE=1,BC的长为2
| 6 |
| 3 |
看了 在Rt△ABC中,∠C=90...的网友还看了以下:
求几道关于三角函数、等比数列的数学题,1.已知函数f(x)=4cosxsin(x+π/6)-1.求 2020-06-02 …
语文语段概括我们又何尝不是这样.我们漫不经心地“建造”自己的生活,不是积极行动,而是消极应付,凡事 2020-06-05 …
已知Ksp(PbBr2)=8.9*10^-6.求PbBr2在纯水中的溶解度.与同离子效应有关系吗? 2020-06-05 …
求思路,关于排列组合的某法院刑事审判第一庭有6位工作人员,现需要选出3位分别参与乒乓球、羽毛球求思 2020-06-12 …
一个一次函数问题如图所示:在直角平面坐标内,点A的坐标是(4,0),第一象限内动点P在直线X+Y= 2020-06-14 …
例4求函数f(x,y)=x3-y3+3x2+3y2-9x的极值.解方程组,求得x=1,-3;y=0 2020-07-31 …
在总体中N~(7.6,4)抽取容量为n的样本如果要求样本均值落在(5.6在总体中N~(7.6,4) 2020-08-03 …
请问在三角形ABC中,角C等于90°,AC等于6,.在三角形ABC中,角C等于90°,AC等于6, 2020-08-03 …
一段话的英译汉生活好比盖房子,每天敲进去一颗钉,加上去一块板,或者竖起一面墙,我们是否每天都在漫不经 2020-11-04 …
求6低透光热反射+12A+6透明和6低透光LOW-E+12A+6透明的中空玻璃的区别具体在哪?节能检 2020-12-09 …