早教吧作业答案频道 -->数学-->
在△ABC中,AC=BC,∠C=90°,将一块等腰直角三角尺的直角顶点放在斜边AB的中点P处,绕点P旋转(1)如图1,三角尺的两条直角边分别交边AC,BC于D,E两点,求证:△PDE为等腰三角形.(2)如
题目详情
在△ABC中,AC=BC,∠C=90°,将一块等腰直角三角尺的直角顶点放在斜边AB的中点P处,绕点P旋转
(1)如图1,三角尺的两条直角边分别交边AC,BC于D,E两点,求证:△PDE为等腰三角形.
(2)如图2,三角尺的两条直角边分别交射线AC,射线BC于D,E两点.(1)中的结论还成立吗?请说明理由.
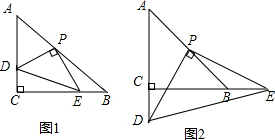
(1)如图1,三角尺的两条直角边分别交边AC,BC于D,E两点,求证:△PDE为等腰三角形.
(2)如图2,三角尺的两条直角边分别交射线AC,射线BC于D,E两点.(1)中的结论还成立吗?请说明理由.

▼优质解答
答案和解析
(1)证明:连接CP,如图1所示: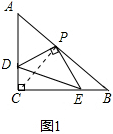
∵AC=BC,∠C=90°,P为斜边的中点,
∴PC⊥AB,PC=
AB=PB,∠PCD=∠B=45°,
∴∠BPE+∠EPC=90°,∠DPC+∠EPC=90°,
∴∠BPE=∠PCD,
在△PBE和△PCD中,
,
∴△PBE≌△PCD(ASA),
∴PE=PD,
即△PDE为等腰三角形;
(2)结论成立;理由如下:
连接CP,如图所示: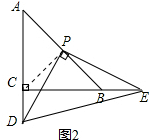
由(1)得:∠BPE=∠PCD,∠PCD=90°+45°=135°,∠PBE=180°-45°=135°,
∴∠PCD=∠PBE,
同(1)可证:△PBE≌△PCD(ASA),
∴PE=PD,
即△PDE为等腰三角形.

∵AC=BC,∠C=90°,P为斜边的中点,
∴PC⊥AB,PC=
| 1 |
| 2 |
∴∠BPE+∠EPC=90°,∠DPC+∠EPC=90°,
∴∠BPE=∠PCD,
在△PBE和△PCD中,
|
∴△PBE≌△PCD(ASA),
∴PE=PD,
即△PDE为等腰三角形;
(2)结论成立;理由如下:
连接CP,如图所示:

由(1)得:∠BPE=∠PCD,∠PCD=90°+45°=135°,∠PBE=180°-45°=135°,
∴∠PCD=∠PBE,
同(1)可证:△PBE≌△PCD(ASA),
∴PE=PD,
即△PDE为等腰三角形.
看了 在△ABC中,AC=BC,∠...的网友还看了以下:
如图,A点、B点分别表示小岛码头、海岸码头的位置,离B点正东方向的7.00km处有一海岸瞭望塔C, 2020-05-13 …
如图所示,杠杆AB的A点挂边长为2dm、密度为ρ1=2kg/dm3的正方体C,B点挂边长为1dm正 2020-05-16 …
如图,A点和B点分别是长方形的两条边的中点,空白部分的面积占这个长方形面积的%,阴影部分面积占这个 2020-06-14 …
(2011•平谷区二模)如图所示,杠杆AB的A点挂边长为2dm、密度为ρ1=2kg/dm3的正方体 2020-06-15 …
根据地球公专示意图[图中左边是a点]南边是b点右边是c点北边是d点图中四点所表示的节气是?图中ab 2020-07-16 …
如图所示,在水平面上有P、Q两点,A、B点分别在P、Q点的正上方,距离地面的高度分别为h1和h2. 2020-07-20 …
画一画,量一量,你有什么发现?(1)过A点分别画已知角的两条边的平行线,得到以A为顶点的角有什么特 2020-07-22 …
A点和B点分别是长方形的两条边的中点.空白部分面积占这个长方形面积的()分之(),阴影部分面积占空白 2020-12-05 …
最短航线问题为什么在北半球当A点在B点东边时从B到A要先西北在东再西南?那它要往西北多少千米往东多少 2020-12-05 …
如图所示为哈雷慧星轨道示意图,A点和B点分别为其轨道的近日点和远日点,则关于哈雷慧星的运动下列判断正 2020-12-24 …