早教吧作业答案频道 -->数学-->
如图1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,ACB的顶点A在△ECD的斜边DE上(1)求证:AE2+AD2=2AC2;(2)如图2,若AE=2,AC=25,点F是AD的中点,直接写出CF
题目详情
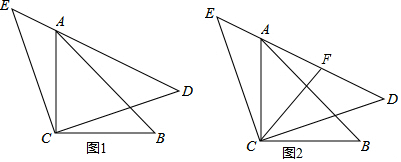
如图1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,ACB的顶点A在△ECD的斜边DE上
(1)求证:AE2+AD2=2AC2;
(2)如图2,若AE=2,AC=2
,点F是AD的中点,直接写出CF的长是___.
(1)求证:AE2+AD2=2AC2;
(2)如图2,若AE=2,AC=2
| | 5 |

▼优质解答
答案和解析
(1)证明:连结BD,如图所示: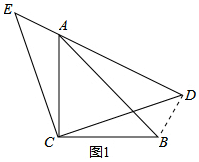
∵△ACB与△ECD都是等腰直角三角形,
∴∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,EC=DC,AC=BC,AC2+BC2=AB2,
∴2AC2=AB2.
∵∠ECD-ACD=∠ACB-∠ACD,
∴∠ACE=∠BCD.
在△AEC和△BDC中,
,
∴△AEC≌△BDC(SAS).
∴AE=BD,∠E=∠BDC=45°,CE=CD,
∴∠BDA=∠BDC+∠ADC=90°,
在Rt△ADB中.∵AD2+BD2=AB2,
∴AD2+AE2=2AC2.
(2) 由(1)得:CE=CD,AE2+AD2=2AC2;
∴∠E=∠CDA,22+AD2=2×(2
)2,
解得:AD=4,
∵点F是AD的中点,
∴AF=DF=2=AE,
∴EF=DA,
在△CEF和△CDA中,
,
∴△CEF≌△CDA(SAS),
∴CF=CA=2
;
故答案为:2
.

∵△ACB与△ECD都是等腰直角三角形,
∴∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,EC=DC,AC=BC,AC2+BC2=AB2,
∴2AC2=AB2.
∵∠ECD-ACD=∠ACB-∠ACD,
∴∠ACE=∠BCD.
在△AEC和△BDC中,
|
∴△AEC≌△BDC(SAS).
∴AE=BD,∠E=∠BDC=45°,CE=CD,
∴∠BDA=∠BDC+∠ADC=90°,
在Rt△ADB中.∵AD2+BD2=AB2,
∴AD2+AE2=2AC2.
(2) 由(1)得:CE=CD,AE2+AD2=2AC2;
∴∠E=∠CDA,22+AD2=2×(2
| 5 |
解得:AD=4,
∵点F是AD的中点,
∴AF=DF=2=AE,
∴EF=DA,
在△CEF和△CDA中,
|
∴△CEF≌△CDA(SAS),
∴CF=CA=2
| 5 |
故答案为:2
| 5 |
看了 如图1,△ACB和△ECD都...的网友还看了以下:
导数中dydxdu的d是什么意思?看书中看到求导公式的时候下面突然冒出来的公式dydxdu等不知道 2020-05-13 …
You"d better中的"d是什么意思? 2020-05-14 …
y=f(x)(xεD)这里的D是什么意思? 2020-05-15 …
关于天体系统的叙述,错误的是B.星系是最高一级天体系统D.目前,总星系的半径大约为200亿光年但我 2020-05-16 …
若a=2010x+2008,b=2010x+2009,c=2010x+2010,则多项式a²+b² 2020-05-16 …
4*4箍筋中内箍筋长度=((B-2*保护层-d)/3*1+d+(H-2*保护层-d)/3*1+d) 2020-05-21 …
根据质量管理的基本原理,PDCA 循环中的“D”是指()。A.计划B.实施C.检查D.处理 2020-05-26 …
全面质量管理中的四个环节中的D是指( )。A.计划B.执行C.检查D.处理 2020-05-31 …
英文的'd是什么意思像这样的we'dI'd一点加个d是甚麼意思 2020-06-08 …
A.B.C.D中有一个人是小偷一个人说的真话。请问是谁。A:不是我偷的B:是A偷的C:不是我A.B 2020-06-08 …